2D shapes and their properties
-

-
 problem
problemSpirostars
A spiropath is a sequence of connected line segments end to end taking different directions. The same spiropath is iterated. When does it cycle and when does it go on indefinitely? -
 problem
problemHexapentagon
Weekly Problem 53 - 2007
The diagram shows a regular pentagon and regular hexagon which overlap. What is the value of x? -
 problem
problemAngle to Chord
Weekly Problem 23 - 2008
A triangle has been drawn inside this circle. Can you find the length of the chord it forms? -
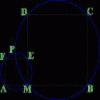 problem
problemCircumspection
M is any point on the line AB. Squares of side length AM and MB are constructed and their circumcircles intersect at P (and M). Prove that the lines AD and BE produced pass through P. -
 problem
problemSquare Areas
Can you work out the area of the inner square and give an explanation of how you did it? -
 problem
problemSquare Pegs
Which is a better fit, a square peg in a round hole or a round peg in a square hole? -
 problem
problemFrom All Corners
Straight lines are drawn from each corner of a square to the mid points of the opposite sides. Express the area of the octagon that is formed at the centre as a fraction of the area of the square. -
 problem
problem2001 Spatial Oddity
With one cut a piece of card 16 cm by 9 cm can be made into two pieces which can be rearranged to form a square 12 cm by 12 cm. Explain how this can be done. -
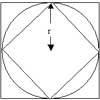 problemFavourite
problemFavouriteApproximating Pi
By inscribing a circle in a square and then a square in a circle find an approximation to pi. By using a hexagon, can you improve on the approximation?
