Efficient cutting
Use a single sheet of A4 paper and make a cylinder having the greatest possible volume. The cylinder must be closed off by a circle at each end.
Problem
Efficient Cutting printable sheet
Cylindrical containers, like the tin cans used to package some food, can be made by using two circles for the ends, and a rectangle which wraps round to form the body.
To make cylinders of varying sizes, the three pieces can be cut from a single rectangle of flat sheet in several ways.
For example:
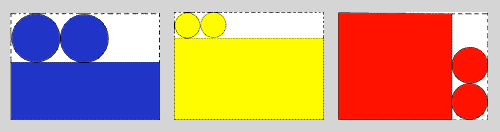
Can you work out some possible dimensions of a rectangle and two circles which can be cut from a single sheet of A4 paper and put together to make a cylinder?
Which dimensions allow you to make a cylinder with the greatest volume?
You can assume that the dimensions of an A4 sheet of paper are 21cm and 29.6cm
Click here for a poster of this problem.
Getting Started
The width of the A4 sheet could determine the circumference of the base of the cylinder. Then the diameter of the base restricts how high the cylinder can be - can you work out the dimensions of this cylinder?
The length of the A4 sheet could determine the circumference of the base of the cylinder.
The width of the A4 sheet could determine the height of the cylinder.
The length of the A4 sheet could determine the height of the cylinder.
Student Solutions
Ysanne and Joanna from Central Newcastle High School sent us their thoughts:
Roughly half of the paper should be used to make the circles and roughly half to make the rectangle as the height of the cylinder and the area of the circle are equally important in creating the volume.
We decided to use the side of length $29.6$ as the circumference of the cylinder. As this was the circumference of the cylinder, and therefore the circles, we divided $29.6$ by $\pi$ to find the appropriate diameter for the circles. This came to $9.42$, so the remaining paper left for the rectangle meant that the height of the cylinder would be 11.58. To find the volume, we found the area of the circle and multiplied by the height of the cylinder: $\pi \times 4.71^2 \times 11.58 \approx 807.5$ cubic centimetres as our volume.
Lyman from Nanjing International School sent us this different arrangement and another similar arrangement for the circles and rectangles to try to maximise the area - click here to see them.
Aleksei's students at CIS Russia used the original sides of the A4 sheets of paper to be the heights of the cylinders, rather than the circumferences of the circles. They managed to get even larger areas:

$\begin{align}&C = 2\pi r = 210 - 2r\\ \Rightarrow &2\pi r +2r = 210\\ \Rightarrow & 2(\pi + 1)r = 210 \\ \Rightarrow & r = 210\div((\pi + 1)\times2)\\ \Rightarrow & r = 25.353 \end{align}$
This gives volume:
$V = \pi r^2h = \pi\times25.353^2\times297 = 599722$ cubic millimetres, or $599.7$ cubic centimetres.

Or:
$\begin{align}&C = 2\pi r = 297 - 2r\\ \Rightarrow &2\pi r +2r = 297\\ \Rightarrow & 2(\pi + 1)r = 297 \\ \Rightarrow & r = 297\div((\pi + 1)\times2)\\ \Rightarrow & r = 35.856 \end{align}$
This gives volume:
$V = \pi r^2h = \pi\times35.856^2\times297 = 848178$ cubic millimetres, or $848.2$ cubic centimetres.
Note that taking the longer side of the A4 sheet of paper to be 296mm instead of 297mm gives the volume as 842.4 cubic centimetres.
Teachers' Resources
Why do this problem?
This problem offers an opportunity for students to apply their knowledge of areas and circumferences of circles, and volumes of cylinders.
Possible approach
This printable worksheet may be useful: Efficient Cutting.
This is an ideal problem for students to tackle in groups of four. Allocating these clear roles (Word, pdf) can help the group to work in a purposeful way - success on this task should be measured by how effectively the group work together as well as by the solution they reach.
- Every group is given a couple of minutes to report back to the whole class. Students can seek clarification and ask questions. After each presentation, students are invited to offer positive feedback. Finally, students can suggest how the group could have improved their work on the task.
- Everyone's posters are put on display at the front of the room, but only a couple of groups are selected to report back to the whole class. Feedback and suggestions can be given in the same way as above. Additionally, students from the groups which don't present can be invited to share at the end anything they did differently.
- Two people from each group move to join an adjacent group. The two "hosts" explain their findings to the two "visitors". The "visitors" act as critical friends, requiring clear mathematical explanations and justifications. The "visitors" then comment on anything they did differently in their own group.
Key questions
Possible extension
Possible support
Sharing this image with students may provide inspiration for different ways of making cylinders.

If students have not met or are not confident with volume of cylinders, they could instead work on the easier problem Cuboid Challenge in the same way.
