KS1 Roadshow

game

Two Stones

This game is known as Pong hau k'i in China and Ou-moul-ko-no in Korea. Why not challenge a friend to play it with you?

problem

Favourite

A City of Towers

Age

5 to 7

Challenge level

In this town, houses are built with one room for each person. There are some families of seven people living in the town. In how many different ways can they build their houses?

problem

Favourite

Number Detective

Age

5 to 11

Challenge level

Follow the clues to find the mystery number.

problem

Skip Counting

Age

5 to 7

Challenge level

Find the squares that Froggie skips onto to get to the pumpkin patch. She starts on 3 and finishes on 30, but she lands only on a square that has a number 3 more than the square she skips from.

Two flowers with the numbers 15 and 16 on them

problem

Favourite

Butterfly Flowers

Age

5 to 7

Challenge level

Can you find two butterflies to go on each flower so that the numbers on each pair of butterflies adds to the number on their flower?

problem

Favourite

Domino Sequences

Age

5 to 7

Challenge level

Find the next two dominoes in these sequences.

problem

Favourite

Nim-7

Age

5 to 11

Challenge level

Can you work out how to win this game of Nim? Does it matter if you go first or second?

problem

Favourite

What Shape and Colour?

Age

5 to 7

Challenge level

Can you fill in the empty boxes in the grid with the right shape and colour?

problem

Favourite

Share Bears

Age

5 to 7

Challenge level

Yasmin and Zach have some bears to share. Which numbers of bears can they share so that there are none left over?

problem

Favourite

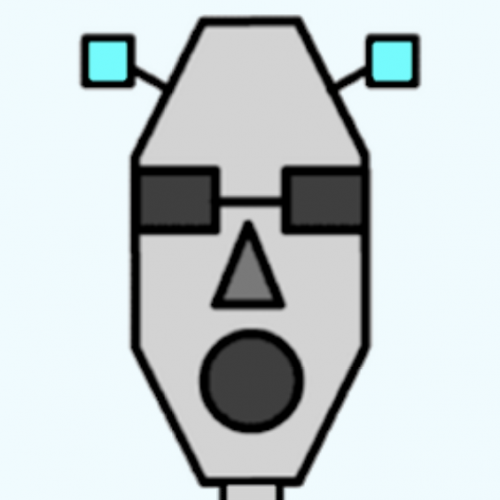
Robot Monsters

Age

5 to 7

Challenge level

Use these head, body and leg pieces to make Robot Monsters which are different heights.

problem

Favourite

Sort the Street

Age

5 to 7

Challenge level

Sort the houses in my street into different groups. Can you do it in any other ways?

problem

Favourite

A resource to try once children are familiar with number lines, and they have begun to use them for addition. It could be a good way to talk about subtraction. Leah and Tom each have a number line. Can you work out where their counters will land?

problem

Favourite

Two-digit targets

Age

5 to 7

Challenge level

You have a set of the digits from 0 to 9. Can you arrange these in the five boxes to make two-digit numbers as close to the targets as possible?

problem

Favourite

What is the time?

Age

5 to 11

Challenge level

Can you put these times on the clocks in order? You might like to arrange them in a circle.

problem

Favourite

Incey Wincey Spider

Age

5 to 7

Challenge level

You'll need two dice to play this game against a partner. Will Incey Wincey make it to the top of the drain pipe or the bottom of the drain pipe first?

problem

Favourite

Seeing Squares

Age

5 to 11

Challenge level

Players take it in turns to choose a dot on the grid. The winner is the first to have four dots that can be joined to form a square.

problem

Favourite

Four Triangles Puzzle

Age

5 to 11

Challenge level

Cut four triangles from a square as shown in the picture. How many different shapes can you make by fitting the four triangles back together?

problem

Favourite

Two Dice

Age

5 to 7

Challenge level

Find all the numbers that can be made by adding the dots on two dice.

problem

Favourite

Biscuit Decorations

Age

5 to 7

Challenge level

Andrew decorated 20 biscuits to take to a party. He lined them up and put icing on every second biscuit and different decorations on other biscuits. How many biscuits weren't decorated?

problem

Whose Face?

Age

5 to 11

Challenge level

These are the faces of Will, Lil, Bill, Phil and Jill. Use the clues to work out which name goes with each face.

problem

Favourite

Next Domino

Age

5 to 7

Challenge level

Which comes next in each pattern of dominoes?

problem

Teddy Bear Line-Up

Age

5 to 7

Challenge level

What is the least number of moves you can take to rearrange the bears so that no bear is next to a bear of the same colour?

problem

Favourite

Missing Middles

Age

5 to 7

Challenge level

Can you work out the domino pieces which would go in the middle in each case to complete the pattern of these eight sets of three dominoes?

problem

Favourite

Making Sticks

Age

5 to 7

Challenge level

Kimie and Sebastian were making sticks from interlocking cubes and lining them up. Can they make their lines the same length? Can they make any other lines?

problem

Domino Join Up

Age

5 to 7

Challenge level

Can you arrange fifteen dominoes so that all the touching domino pieces add to 6 and the ends join up? Can you make all the joins add to 7?

problem

Four Colours

Age

5 to 11

Challenge level

Kate has eight multilink cubes. She has two red ones, two yellow, two green and two blue. She wants to fit them together to make a cube so that each colour shows on each face just once.

problem

Favourite

Make 37

Age

5 to 11

Challenge level

Four bags contain a large number of 1s, 3s, 5s and 7s. Can you pick any ten numbers from the bags so that their total is 37?

problem

Tangrams

Age

5 to 11

Challenge level

Can you make five differently sized squares from the interactive tangram pieces?

problem

Teddy Town

Age

5 to 11

Challenge level

There are nine teddies in Teddy Town - three red, three blue and three yellow. There are also nine houses, three of each colour. Can you put them on the map of Teddy Town according to the rules?

problem

Three block towers

Age

5 to 7

Challenge level

Take three differently coloured blocks - maybe red, yellow and blue. Make a tower using one of each colour. How many different towers can you make?

problem

Teddy Town - Part two

Age

5 to 11

Challenge level

There are nine teddies in Teddy Town - three red, three blue and three yellow. There are also nine houses, three of each colour. Can you put them on the map of Teddy Town according to the rules?

problem

Ladybird Box

Age

5 to 11

Challenge level

Place six toy ladybirds into the box so that there are two ladybirds in every column and every row.

problem

Teddy Town - Part three

Age

5 to 11

Challenge level

There are sixteen teddies in Teddy Town - four red, four blue, four yellow and four green. There are also sixteen houses, four of each colour. Can you put them on the map of Teddy Town according to the rules?

problem

Teddy Town - Part four

Age

5 to 11

Challenge level

There are twenty five teddies in Teddy Town - five red, five blue, five yellow, five green and five purple. There are also twenty five houses, five of each colour. Can you put them on the map of Teddy Town according to the rules?

problem

Teddy Town - Part five

Age

5 to 11

Challenge level

There are thirty six teddies in Teddy Town - six red, six blue, six yellow, six green, six purple and six turquoise. There are also thirty six houses, six of each colour. Can you put them on the map of Teddy Town according to the rules?

problem

Three by Three

Age

5 to 11

Challenge level

Arrange 3 red, 3 blue and 3 yellow counters into a three-by-three square grid, so that there is only one of each colour in every row and every column

problem

Favourite

Mixed-up Socks

Age

5 to 7

Challenge level

Start with three pairs of socks. Now mix them up so that no mismatched pair is the same as another mismatched pair. Is there more than one way to do it?

problem

Three Way Mix Up

Age

5 to 11

Challenge level

Jack has nine tiles. He put them together to make a square so that two tiles of the same colour were not beside each other. Can you find another way to do it?