Skip Counting
Find the squares that Froggie skips onto to get to the pumpkin patch. She starts on 3 and finishes on 30, but she lands only on a square that has a number 3 more than the square she skips from.
Age
5 to 7
Challenge level
Find the squares that Froggie skips onto to get to the pumpkin patch.
She starts on $3$ and finishes on $30$, but she lands only on a square that has a number $3$ more than the square she skips from.
Image
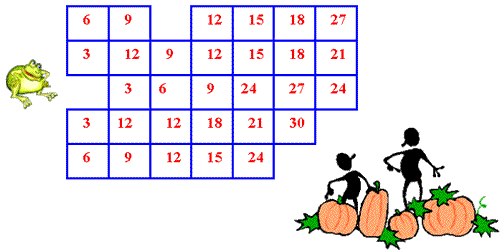
Is there more than one way that Froggie can get to the pumpkins?
Printable NRICH Roadshow resources: Instructions and GameboardsYou could help the pumpkin people get to Froggie by starting at $30$ and travelling to $3$, always skipping onto a square that is $3$ less than the square they have skipped from.
Alison and Anne of St John's Primary School sent us in their answers:
Image
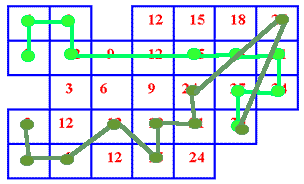
Image
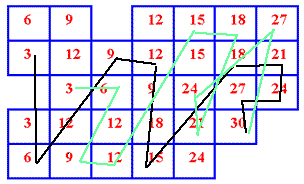
They also explained what they thought would limit the number of possible paths.
There are only two $27$ squares, but there are three of every other square apart from $30$, so if you want different paths to have every square apart from $30$ different, you can only have two because there are only two $27$s. If it is okay to have more than just the $30$ the same, then it is still the $27$s that will limit the number of paths that is possible.
And Jamie, aged 7, told us:
You do not need to find paths for the pumpkin people to take to catch Froggie, because any path she takes they can take and any path she can't take they can't take, they just go in the opposite direction. This is because counting down in threes gives you the same numbers as counting up in threes just in the opposite order
Thank you very much, Jamie, Alison and Anne!
Skip Counting
Find the squares that Froggie skips onto to get to the pumpkin patch.
She starts on $3$ and finishes on $30$, but she lands only on a square that has a number $3$ more than the square she skips from.
Image
Is there more than one way that Froggie can get to the pumpkins?
Why do this problem?
This problem provides an appealing context for practising the three times table. It gives an opportunity for children to realise that there is not necessarily just one answer to a mathematical problem.
Children might find it helpful to use this sheet of the grid with counters.
Key questions
How are you deciding where to go?
Which square could we go to next?
Do you think there are more than one route?
If so, how you you find it?
Is there a way of remembering your route?
Do you think there are more than one route?
If so, how you you find it?
Is there a way of remembering your route?