Four colours
Kate has eight multilink cubes. She has two red ones, two yellow, two green and two blue. She wants to fit them together to make a cube so that each colour shows on each face just once.
Problem
Kate has eight multilink cubes. She has two red ones, two yellow, two green and two blue.
Image

She wants to fit them together to make a cube so that each colour shows on each face just once.
Image
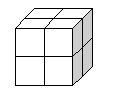
Is it possible ?
If so, how?
If you've found a way, is there another way?
Printable NRICH Roadshow resource.
If you want more of a challenge, have a look at this problem:
Getting Started
How many faces on a cube?
How many small faces can you see on each of the larger faces?
How many small faces can you see on the larger cube?
How does this compare with the number of small faces there are altogether?
Can you explain what you notice?
How many faces of each of the smaller cubes will be visible on the larger cube?
How many small faces can you see on each of the larger faces?
How many small faces can you see on the larger cube?
How does this compare with the number of small faces there are altogether?
Can you explain what you notice?
How many faces of each of the smaller cubes will be visible on the larger cube?
Student Solutions
Daniel from Bolney CEP School wrote saying the following and included a picture:
I found out that you had to start with all four colours on one face. Then I made sure I worked diagonally with the other colours. This meant that all faces could show all four colours.
Image

Julian from the British School Manila in the Philippines sent in the following solution:
Top face:
R Y
G B
Left face:
R G
Y B
Right face:
Y B
R G
Bottom face:
(imagine you could see through the top)
Y G
B R
Back face:
B R
G Y
Thank you and well done! If you thought it was impossible, have a think about those solutions above.
Teachers' Resources
Why do this problem?
This practical problem can be very engaging. It has the ability to introduce pupils to some logical reasoning as well as being solvable by trial and improvement.
Possible approach
You could put eight cubes (of the correct colours) together to make a large cube without there being one of each colour on each face. Ask children what they notice. Give time for them to consider this individually then suggest they talk with a partner. Finally, you can draw the whole group together to share ideas.
Hopefully that initial discussion will have brought up some of the attributes of the large cube so you can introduce learners to the challenge itself. Plenty of cubes will be required for children to try out their ideas.
After a short time, bring everyone together for a 'mini plenary' where progress is discussed. This can help children articulate their ideas so far and it gives others a helping hand if they have found it hard to get started.
In the plenary, you could ask a few pupils to share some particularly useful ways of approaching this problem, perhaps because they have worked systematically.
Hopefully that initial discussion will have brought up some of the attributes of the large cube so you can introduce learners to the challenge itself. Plenty of cubes will be required for children to try out their ideas.
After a short time, bring everyone together for a 'mini plenary' where progress is discussed. This can help children articulate their ideas so far and it gives others a helping hand if they have found it hard to get started.
In the plenary, you could ask a few pupils to share some particularly useful ways of approaching this problem, perhaps because they have worked systematically.
Key questions
How are you trying to solve this?
Have you checked each face has one of each colour cube?
Possible support
Having a collection of coloured cubes available will help all children have a go at this problem.
