Making Sticks
1 out of 3
Kimie and Sebastian were making sticks from interlocking cubes and lining them up. Can they make their lines the same length? Can they make any other lines?
Problem
Printable NRICH Roadshow resource
Kimie and Sebastian were making sticks from interlocking cubes. Kimie made blue sticks two cubes long. Sebastian made red sticks three cubes long. They both made a lot of sticks.
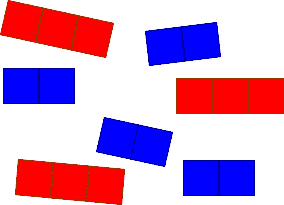
Kimie put her blue sticks end to end in a long line. Sebastian put his red sticks end to end in a line underneath Kimie's.
Can they make their lines the same length? How many sticks could Kimie use? How many would Sebastian put down? How long is the line altogether?
Can they make any other lines?
Getting Started
You could use cubes to make the sticks yourself, or draw the sticks on squared paper.
If you line up two blue sticks, can you make a line of red sticks which is the same length?
Try with three blue sticks - can you make a line of red sticks which is the same length?
What happens when you try four blue sticks? Five?
Student Solutions
We received a lot of excellent solutions to this activity. Thank you to everybody who shared their ideas with us.
Grace from William Konkin Elementary School in Canada drew this picture to represent one possible solution:
This is very clear, Grace, and I can see that these two lines of sticks are both of length six. I wonder why three blue sticks are equal to two red sticks?
Chaffinches Class from Anston Greenlands Primary School in England noticed something about the lengths of the blue and the red sticks:
We found that there is a pattern to make the sticks the same length. Roman discovered that the red sticks were going up in 2's and the blue sticks were going up in 3's. We managed to predict the next series of sticks needed to make the red and blue sticks the same length.
Akash from Cottenham School in England found the next solution after 6, and noticed a pattern:
The blues could make 12 and the reds could make 12. They could both make 6, 12, 18, 24, 30, 36. Each one of these is six more than the one before. The pattern is multiplying even numbers by three.
It does seem to be going up by 6 each time. I wonder why the pattern involves multiplying even numbers by 3?
Lots of children from William Konkin Elementary School sent in their thoughts about this problem. Oscar also noticed that the solution had to be an even number, and that they were going up by 6 each time:
Sienna drew a diagram to represent this:
Valan from The GYM Foundation in the UK worked systematically through some of the solutions:
This is interesting - it looks like there need to be an even number of red sticks, which is similar to Oscar's idea about the length needing to be even. Take a look at Valan's full solution to see more of their ideas about this problem.
Lizzie from Alleyn's Junior School in the UK found two different ways of describing the pattern:
They can make an infinite number of lines that are the same length. The length of any line has to be in the 6 times table. It could also be any even number in the 3 times table it is the same thing as the six times table.
We also received a lot of ideas about this problem from the children at Ganit Kreeda in Vichar Vatika, India. Avic had some more ideas about odd and even numbers, and explained that the length will be a number that is both a multiple of 2 and a multiple of 3:
Kimie’s stick can only make even numbers because all the multiples of 2 are even. There is a pattern in Sebastian’s sticks, it is odd-even-odd-even. They can make the lines the same lengths because when you multiply 2x3 you get 6.
Kanaa noticed that 6 is the lowest common multiple of 2 and 3 (the smallest number in both the 2 and the 3 times table):
When they make a multiple of 6, their sticks would be of the same length. 6=2x3 and the lowest common multiple of 2 and 3
K - 6 (3 sticks)
S - 6 (2 sticks)
Thank you all for your thoughts about this - it looks like there are lots of lines Kimie and Sebastian can make, as long as their lines are in the 6 times table! We also received similar ideas from: Adhvaith from The GYM Foundation in India; Adam from Copthorne Preparatory School in England; Ruhi, Mrunmayee, Kimaya, Reyansh, Advaya and Aarav from Ganit Kreeda in Vichar Vatika, India; Quinn, Wyatt, Mica, Audrey B, Audrey R, Milo, Henrik, Skyler, Tristan, Morgan, Stasa, Greyson, Aubree, Darragh, Ella, Kenzie and Sharvil from William Konkin Elementary School in Canada; and Atharvv from Pupil Tree School in Ballari, India.
Teachers' Resources
Using NRICH Tasks Richly describes ways in which teachers and learners can work with NRICH tasks in the classroom.
Why do this problem?
This problem encourages children to use counting-on techniques, but offers you an opportunity to introduce them to the idea of multiples.
Possible approach
Having cubes available for the children to use is a necessary part of this problem, as it makes it accessible to all. One way to introduce it would be for children to work in pairs, one of them making blue sticks (each of two cubes) and one making red sticks (each using three cubes), although of course the colour isn't important. Then, pose the questions in the problem for them to investigate together. (Depending on the kind of cubes you have, you may want the children to actually attach the sticks to each other, as just lining them up may mean that you cannot get them close enough together.) You could ask children to record their working, perhaps on squared paper by colouring squares.
Talking to the group about total lengths of blue sticks which match lengths of red sticks allows you to model the appropriate language, for example "$6$ is a multiple of $2$ and $6$ is also a multiple of $3$". However, it has a lot of scope to be taken further - the open-ended nature of the activity also allows children to make a generalisation about all the lengths of sticks that can be made from both blue and red. Although many may not be able to verbalise this formally, they will certainly be able to look for patterns in the numbers that are possible and this can lead to a fruitful discussion.
This work would make a lovely display, for example using sticky red and blue squares on a large grid.
Key questions
How many cubes have you used in this line? And this line?
Can you find any other lines that are the same length as each other?
What is the next line that can be made from both red and blue sticks? How do you know?
Possible extension
Some pupils could investigate sticks of two different lengths, for example 2 and 5; or even three different lengths.
Possible support
Some children may have difficulty keeping track of the number of sticks they have joined together. It would be worth you talking about strategies to help with this, such as counting in threes once a long line has been constructed.