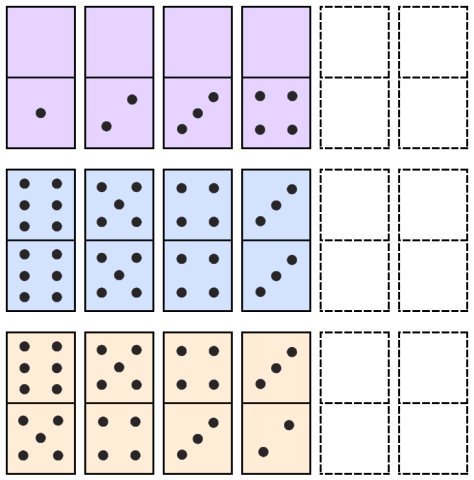
Next domino
Problem
Getting Started
Student Solutions
0 0 0 0 : 0 0
1 2 3 4 : 5 66 5 4 3 : 2 1
6 5 4 3 : 2 16 5 4 3 : 2 1
5 4 3 2 : 1 0
Bora from Irmak Primary School, Turkey used some excellent words to describe the patterns.
1st row: 5 and 6, because they are in decreasing order.
2nd row: 2-2 and 1-1, again in decreasing order, this time in doubles.
3rd row: 2-1 and 1-0, again in decreasing order, but both parts are full, upper part goes from 6 to 1, lower from 5 to 0.
Teachers' Resources
Why do this problem?
This problem is an appealing way for children to recognise, interpret, describe and extend number sequences. Developing their own patterns, as in the later part of the activity, provides an opportunity for them to justify their own thinking, and evaluate others' patterns.
Possible approach
The children should be familiar with dominoes through free-play and domino games before attempting more formal tasks such as pattern building.
It would be good to gather the group on the carpet using large floor dominoes for this activity, or alternatively use virtual dominoes on the interactive whiteboard which you can drag around the screen (you might find our Dominoes Environment useful). Begin with single patterns as in the first example in the problem, keeping one end of the dominoes constant (as in all sixes, all blanks, all ones etc.). You may want to deliberately get the sequence wrong to challenge pupils to correct your mistake. Encourage them to explain why it is wrong and also why their correction is right.
Key questions
Possible extension
Possible support
Many children will benefit from saying the numbers in the sequence out loud to reinforce the familiar counting patterns.