Year 5 Exploring and Noticing

problem

Favourite

Multiplication squares

Age

7 to 11

Challenge level

Can you work out the arrangement of the digits in the square so that the given products are correct? The numbers 1 - 9 may be used once and once only.

problem

Favourite

Trebling

Age

7 to 11

Challenge level

Can you replace the letters with numbers? Is there only one solution in each case?

problem

Favourite

Brush loads

Age

7 to 11

Challenge level

How can you arrange the 5 cubes so that you need the smallest number of Brush Loads of paint to cover them? Try with other numbers of cubes as well.

problem

Favourite

The numbers give the design

Age

7 to 11

Challenge level

Make new patterns from simple turning instructions. You can have a go using pencil and paper or with a floor robot.

problem

Favourite

Area and perimeter

Age

7 to 11

Challenge level

What can you say about these shapes? This problem challenges you to create shapes with different areas and perimeters.

problem

Favourite

Multiply multiples 1

Age

7 to 11

Challenge level

Can you complete this calculation by filling in the missing numbers? In how many different ways can you do it?

problem

Favourite

Multiply multiples 2

Age

7 to 11

Challenge level

Can you work out some different ways to balance this equation?

problem

Favourite

Round the dice decimals 2

Age

7 to 11

Challenge level

What happens when you round these numbers to the nearest whole number?

problem

Favourite

Multiply multiples 3

Age

7 to 11

Challenge level

Have a go at balancing this equation. Can you find different ways of doing it?

problem

Favourite

Division rules

Age

7 to 11

Challenge level

This challenge encourages you to explore dividing a three-digit number by a single-digit number.

game

Favourite

Factors and multiples game

A game in which players take it in turns to choose a number. Can you block your opponent?

problem

Favourite

Tumbling down

Age

7 to 11

Challenge level

Watch this animation. What do you see? Can you explain why this happens?

problem

Favourite

Compare the calculations

Age

7 to 11

Challenge level

Can you put these four calculations into order of difficulty? How did you decide?

problem

Favourite

Highest and lowest

Age

7 to 11

Challenge level

Put operations signs between the numbers 3 4 5 6 to make the highest possible number and lowest possible number.

problem

Favourite

Xavi's t-shirt

Age

7 to 16

Challenge level

How much can you read into a t-shirt?

problem

Favourite

Abundant numbers

Age

7 to 11

Challenge level

48 is called an abundant number because it is less than the sum of its factors (without itself). Can you find some more abundant numbers?

problem

Favourite

All the digits

Age

7 to 11

Challenge level

This multiplication uses each of the digits 0 - 9 once and once only. Using the information given, can you replace the stars in the calculation with figures?

problem

Favourite

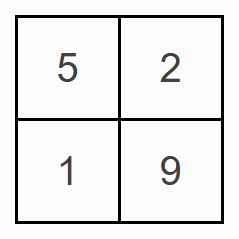
Reach 100

Age

7 to 11

Challenge level

Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.

problem

Favourite

Two primes make one square

Age

7 to 11

Challenge level

Can you make square numbers by adding two prime numbers together?

problem

Favourite

Cycling squares

Age

7 to 11

Challenge level

Can you make a cycle of pairs that add to make a square number using all the numbers in the box below, once and once only?

problem

Favourite

Route product

Age

7 to 11

Challenge level

Find the product of the numbers on the routes from A to B. Which route has the smallest product? Which the largest?

problem

Favourite

Factor track

Age

7 to 11

Challenge level

Factor track is not a race but a game of skill. The idea is to go round the track in as few moves as possible, keeping to the rules.

problem

Favourite

Through the window

Age

7 to 11

Challenge level

My local DIY shop calculates the price of its windows according to the area of glass and the length of frame used. Can you work out how they arrived at these prices?

problem

Favourite

Pouring problem

Age

7 to 11

Challenge level

What do you think is going to happen in this video clip? Are you surprised?

problem

Favourite

Pebbles

Age

7 to 11

Challenge level

Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?

problem

Favourite

Egyptian rope

Age

7 to 11

Challenge level

The ancient Egyptians were said to make right-angled triangles using a rope with twelve equal sections divided by knots. What other triangles could you make if you had a rope like this?

problem

Favourite

Make 100

Age

7 to 11

Challenge level

Find at least one way to put in some operation signs to make these digits come to 100.

problem

Favourite

Forgot the numbers

Age

7 to 11

Challenge level

On my calculator I divided one whole number by another whole number and got the answer 3.125. If the numbers are both under 50, what are they?

problem

Favourite

Numerically equal

Age

7 to 11

Challenge level

Can you draw a square in which the perimeter is numerically equal to the area?

problem

Favourite

Twenty divided into six

Age

7 to 11

Challenge level

Katie had a pack of 20 cards numbered from 1 to 20. She arranged the cards into 6 unequal piles where each pile added to the same total. What was the total and how could this be done?

problem

Favourite

One wasn't square

Age

7 to 11

Challenge level

Mrs Morgan, the class's teacher, pinned numbers onto the backs of three children. Use the information to find out what the three numbers were.

problem

Favourite

Fitted

Age

7 to 11

Challenge level

Nine squares with side lengths 1, 4, 7, 8, 9, 10, 14, 15, and 18 cm can be fitted together to form a rectangle. What are the dimensions of the rectangle?