Pebbles
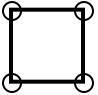
Imagine that you're walking along a sandy beach collecting pebbles. You start off with four pebbles and you place them on the sand as the corners of a square. The area inside your pebbles is just 1 square.
|
|
|
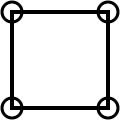
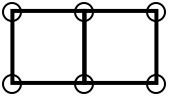
By adding another 2 pebbles you double the area to 2 squares, like this:
|
|
||
|
|
||
|
|
||
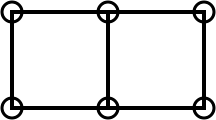
The rule is that you keep the pebbles that you already have, not moving them to any new positions, and add as few new pebbles as necessary to double the previous area.
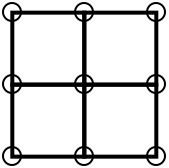
So, to continue, we add another three pebbles to get an area of 4:
|
|
||
|
|
||
|
|
|
|
|
|
||
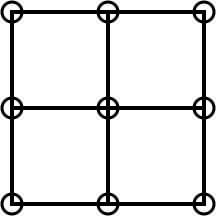
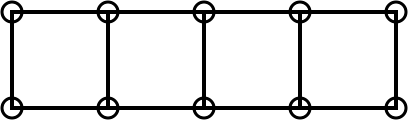
You could have doubled the area by doing this instead:
|
|
|
|
||
|
|
|
|
||
|
|
||||
But this would not be allowed because we are adding as few pebbles as possible each time.
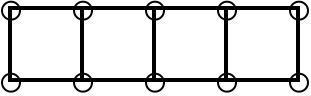
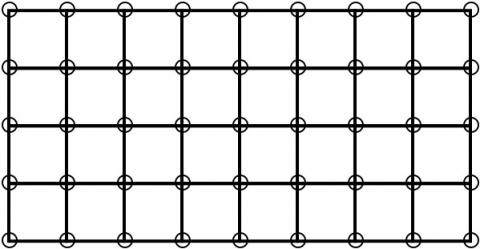
The sixth arrangement of pebbles would look like this:
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
||||||||
Now it's time for you to have a go.
What do you notice about the arrangements? What questions could you ask about them?
You might like to explore:
How many extra pebbles are added each time? This starts off as 2, 3, 6...
How many are there around the edges? This starts off as 4, 6, 8...
How big is the area? This starts off as 1, 2, 4...
How many pebbles are there inside each arrangement? This starts off as 0, 0, 1, 3, 9...
Don't forget the all-important question to ask - "I wonder what would happen if I ...?''
More Pebbles is a three-dimensional version of this task, which you might like to have a go at afterwards.
Can you make a rectangle with just one more pebble? Two more? Three more ...?
Have you checked that each rectangle is double the size of the last one?
How are you recording what you have done?
A group of children from Manorfield Primary School, Stoney Stanton sent in lots of ideas:
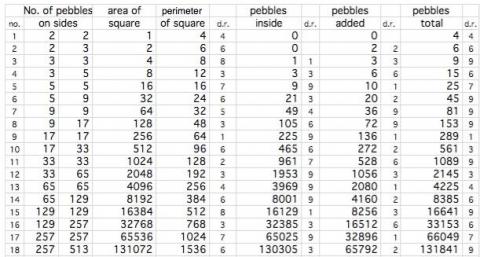
S.B. and N.L. produced the following table of results:
| Number | Shape | Number of pebbles on side | Area of shape | Perimeter of shape |
| 1 | Square | 2x2 | 1cm$^2$ | 4cm |
| 2 | Rectangle | 2x3 | 2cm$^2$ | 6cm |
| 3 | Square | 3x3 | 4cm$^2$ | 8cm |
| 4 | Rectangle | 3x5 | 8cm$^2$ | 12cm |
| 5 | Square | 5x5 | 16cm$^2$ | 16cm |
| 6 | Rectangle | 5x9 | 32cm$^2$ | 24cm |
| 7 | Square | 9x9 | 64cm$^2$ | 32cm |
| 8 | Rectangle | 9x17 | 128cm$^2$ | 48cm |
A.H and E.R also said:
Now, Alice from St Thomas' Church of England Primary School, wrote;
On B (how many pebbles there are round the edges), the pattern starts on 4 adds 2 which makes 6 adds another 2 which is eight then adds 4 which makes 12 adds 4 again (16) adds 8 (24) adds 8 adds 16, and so on.
So it adds one thing twice then doubles the adding number and starts to do that again.
Amelia from NLCS sent in her ideas;
First double forward then double sideways and so on
Pebbles added: 2,3,6,10,20,36,72
Pebbles Outside: 4,6,8,12,16,24,32
Squares: 1,2,4,8,16,32,64,128
Well done all of you - you obviously worked hard on this problem.
Pebbles
Imagine that you're walking along the beach, a rather nice sandy beach with just a few small pebbles in little groups here and there. You start off by collecting just four pebbles and you place them on the sand in the form of a square. The area inside is of course just $1$ square something, maybe $1$ square metre, $1$ square foot, $1$ square finger ... whatever.
By adding another $2$ pebbles in line you double the area to $2$, like this:
The rule that's developing is that you keep the pebbles that are down already (not moving them to any new positions) and add as FEW pebbles as necessary to DOUBLE the PREVIOUS area, using RECTANGLES ONLY!
So, to continue, we add another three pebbles to get an area of $4$:
You could have doubled the area by doing:
But this would not obey the rule that you must add as FEW pebbles as possible each time. So this one is not allowed.
Number 6 would look like this:
So remember:-
The rule is that you keep the pebbles that are down already (not moving them to any new positions) and add as FEW pebbles as necessary to DOUBLE the PREVIOUS area.
Well, now it's time for you to have a go.
"It's easy,'' I hear you say. Well, that's good. But what questions can we ask about the arrangements that we are getting?
We could make a start by saying "Stand back and look at the shapes you are getting. What do you see?'' I guess you may see quite a lot of different things.
It would be good for you to do some more of this pattern. See how far you can go. You may run out of pebbles, paper or whatever you may be using. (Multilink, pegboard, elastic bands with a nail board, etc.)
Well now, what about some questions to explore?
Here are some I've thought of that look interesting:
- How many extra pebbles are added each time? This starts off $2$, $3$, $6$ ...
- How many are there around the edges? This starts off $4$, $6$, $8$ ...
- How big is the area? This starts off $1$, $2$, $4$ ...
- How many are there inside? This starts off $0$, $0$, $1$, $3$, $9$ ...
Try to answer these, and any other questions you come up with, and perhaps put them in a kind of table/graph/spreadsheet etc.
Do let me see what you get - I'll be most interested.
Don't forget the all-important question to ask - "I wonder what would happen if I ...?''
Why do this problem?
Use this activity to introduce children to an investigation that mixes both shape and space work with number work. You could also introduce learners to this extended piece of work to help you look at perseverence and persistence.
Possible approach
A good introduction can be had with the whole class by making the first two or three arrangements all together. It is useful to have squared and dotted (squares) paper available whilst some pupils may benefit from using blocks (such as multilink) to represent the pebbles. You may also find it helpful to use a virtual geoboard for sharing ideas amongst the whole group.
Key questions
Possible extension
Some pupils may produce a table or a spreadsheet of their results which would enable them to explore further.
Alternatively, Making Squares is an extension activity.
For more extension work
Go to More Pebbles.
Possible support
Children may benefit from adult support in keeping track of where they are in their exploration. They could be helped to proceed as if it were a game.