Twenty Divided into Six

We had over seventy solutions sent in for this activity!

Miranda from Redmaids' High Junior School wrote this helpful introduction for the solutions:

There are thousands of different combinations to this puzzle, and this is what makes it seem so difficult - so if you want to narrow the answers down you need to try and use some simple maths to work out what the piles add up to. We'll call it x . We already know that there are the numbers 1-20, and when added they make 210. This can be called y. What has this got to do with x? Well, we need six piles so we need to divide y by 6.  Now insert the formula into a division.

So x = 35! This is very useful. All we need to do is sort the numbers into six piles that each add up to 35. Wait! The six piles have to be unequal. If you did all different numbers of cards, you could have 1+ 2 + 3 + 4 + 5 + 6, which equals 21. 1 card is left over but we know 20, the biggest number, is too small! This means that although the piles are unequal, there need to be some piles with the same number of cards.

We need to get the total of the numbers of cards in each pile just right so that it adds up to 20. For example, 2 + 2 + 3 + 4 + 4 + 5 cards = 20 cards. That means there could be a solution to this combination.

So feel free to go and have an explore! Don't worry if your cards don't add up as there are still lots of ways that you can place them. Here is practical tip that it would be a very good idea to use: Don't put the small numbers in big piles all the time because you need them to 'fill in the gaps' that the big numbers make e.g 19 + 5 + 1.

These are all the pupils who sent in correct solutions:

Sahasra at Reigate Priory School;

Team Boss at Bede Burn School;

Stanley at St John's Primary, Basingstoke;

Dhianat at Holtspur Primary School; 

Jack and Daniel at Crossgates Primary School, Scotland;

Ioan and Kai at Abercanaid, Wales;

Gabo at King's College London in China; 

Joshua and Texas at Bandung Independent School, Indonesia;

Olivia at Marlborough Primary, Wales;

Callum and Micha, Owen and Tye, Thomas and Jessica at Jarrow Cross C of E Primary School; 

Jorja at Raetihi School, New Zealand;

Vivaan at Ridgeway Primary School;

William at Emmbrook Junior School;

Andrew, Nick, Isabelle at Drummoyne Public School, Australia;

Monty at Mawdesley St Peter's; 

Oliver at St John's CEP, Sevenoaks;

Dylan at Plantation Primary;

Lola at Brookfield Primary School;

Miranda at Redmaids' High Junior School;

Dylan at Wharncliffe Side Primary School, Sheffield;

Harvey and Kieran at Westcott Primary School, Hull; 

Shriya at International School Frankfurt, Germany;

Ritesh and Khushi, Felix and Jasmine, Eaven and Izzy, Neya and Dhiyaan, Molly and Dylan, Shania and Cameron, Martha and Mya at Highcliffe Primary School; 

Zara and Gemma at St Cuthbert Mayne; 

A pupil at Barrs Court;

Niamh, Amani, Manahal and Tamara at Saint Augustine's Priory;

Riley and Milan at Lyneham Primary School, Australia;

Matthew, Logan and Hayden, Ben and Harry, Kieran and Owen at Ashfield Junior School;

Naa, Isobel, Thomas, Josh and Isla, Phoebe, Amelia, Jessica and Lily at Thorpe Primary School;

Harvey and Kieran at Westcott Primary School, Hull;

Elsa at Meavy C of E Primary School.

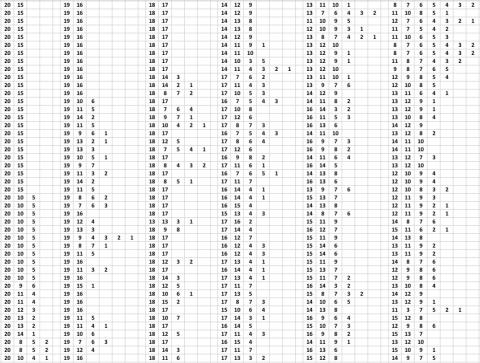
Here are all the correct solutions that came in. This picture can be clicked on to make it bigger.

Image

We have another solution for the 20 divided into six problem. Here's how we did it.

What we did first was add all the numbers on the cards together then we divided it by six. That’s 35. Then we divided 20 by six which is around 3. Then we knew that we had to put around 3 numbers in every box.

We started with the easy one, 20,10,5. Going down by one:

19, 13, 3

18, 15, 2

skipped 17 because we couldn’t find a 3 match

16, 11, 8

15 is already on one

14, 12, 9.

Now that’s 5 so we used the 5 remaining numbers: 1, 4, 6, 7, 17, equalling 35

All of those 6 piles equal 35!!!!!!

Well done both of you - this solution is different from all the ones in the table above!

Dhian from Holtspur Primary School had an interesting adventure with this activity. He wrote:

The groups are: 12, 8 and 2, 7, 6, 5 and 10, 1, 9 and 3, 17 and 20 and 4, 16.

These are the 6 groups and the total they add to is 20. I have not not used all of the numbers from 1 to 20 as the puzzle did not state this (hope that's ok!).

That's an interesting variation!

Well done all of you who sent in good solutions which form part of the chart above.