Area and perimeter
What can you say about these shapes? This problem challenges you to create shapes with different areas and perimeters.
Problem
What can you say about these two shapes?
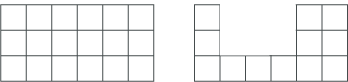
What is the area of each one? What is the perimeter of each one?
What can you say about the shapes below?
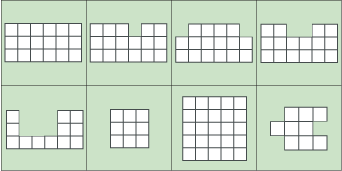
You can print out a set of shapes and cut them into separate cards. These cards have the coloured background.
Can you draw a shape in which the area is numerically equal to its perimeter? And another?
Can you draw a shape in which the perimeter is numerically twice the area?
Can you draw a shape in which the area is numerically twice the perimeter?
Can you make the area of your shape go up but the perimeter go down?
Can you make the perimeter of your shape go up but the area go down?
Can you draw some shapes that have the same area but different perimeters?
Can you draw some shapes that have the same perimeter but different areas?
Getting Started
Using squared paper to sketch shapes might help.
Student Solutions
Matthew from Parkgate Primary School focused on the first two shapes in the problem. He said:
The area of the rectangle is $18$cm$^2$ and its perimeter is $18$cm.
The second shape is $12$cm$^2$ and its perimeter is $22$cm.
Thomas from Colet Court examined the eight shapes which were drawn on the cards. He labelled the shapes A, B, C, D, E, F, G and H, going from left to right in the top row, then left to right in the bottom row.
A: P is 18 , A is 18; B: P is 20 , A is 17; C: P is 18 , A is 16; D: P is 20 , A is 16
E: P is 22 , A is 12; F: P is 12 , A is 9; G: P is 20 , A is 25; H: P is 16 , a is 9
Thomas didn't give any units in his solution. I guess we could say the perimeter is measured in 'units' and the area in 'square units', although some of you, like Matthew above, assumed the squares were 1cm long. So, that would mean the perimeter is in cm and the area in cm$^2$. Thomas remarked:
The perimeter is always bigger except for one (Shape G).
Noor from Kingsbury Green Primary School answered the question; 'Can you draw a shape in which the area is numerically equal to its perimeter? And another?'. He said:
I found if I did $4\times4$ I would get an area of $16$.
If I counted the sides there would be four on each side: $4+4+4+4 = 16$.
The area and perimeter are the same.
The same happened if there you have a rectangle that has a length of $6$ and a width of $3$.
Table 3 (they didn't give their school) looked at finding a shape which has a perimeter numerically twice the area. They wrote:
Bashayer from Kingsbury Green Primary also found this solution. Miiti from Kingsbury Green created this shape which has a perimeter of $20$ units and an area of $10$ square units:
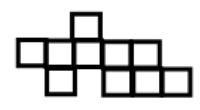
Thomas from Colet Court drew a shape in which the area is numerically twice the perimeter:

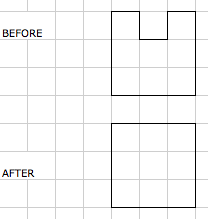
Thomas went on to investigate how to make the area of a shape go up but the perimeter go down. He said:
...you go from a dented square to a square shape.
Thomas also said that you can make the perimeter of a shape go up but the area go down
by inserting a dent in your shape the area gets reduced by the dent.
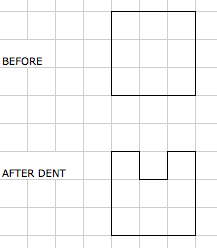
Joe and Charlie from Coniston Primary described the way they worked on this part of the problem:
First we picked a shape which was a square so we looked at the area and perimeter.
The area was $25$cm$^2$ and the perimeter was $20$cm.
We took $1$ chunk out of the top of the square and it did make the perimeter bigger and the area became smaller. The perimeter became bigger because it adds on $2$ more lines so the perimeter became $22$cm.
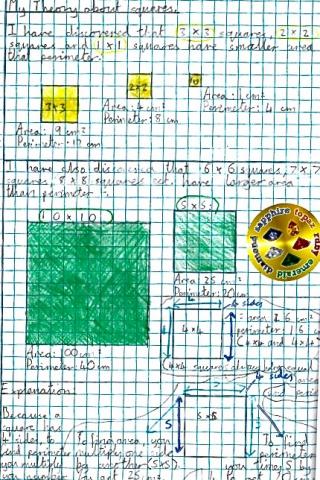
Whilst investigating problem 7280, Anna from Air Balloon Hill Primary made the following observations which she would like to share with you. Please see attachment taken from her exercise book. Year 5 teacher
Very, very well done all of you. You have obviously put a lot of thought into this problem.
Teachers' Resources
Why do this problem?
This problem offers opportunities for children to consolidate their understanding of area and perimeter. The exploratory nature of the task means that learners will be grappling with the two concepts at the same time rather than tackling them independently which might usually be the case. The activity is likely to require persistence and a 'tinkering' or trial and improvement approach.
Possible approach
Key questions
Possible extension
Learners might like to have a go at the Pebbles investigation which makes a good follow-up to this challenge.
Possible support
The problems Sizing Them Up and Wallpaper might be useful starting points for those children who are struggling with the concept of area.
