Symmetry
-

-
 problem
problemHolly
The ten arcs forming the edges of the "holly leaf" are all arcs of circles of radius 1 cm. Find the length of the perimeter of the holly leaf and the area of its surface. -
 problem
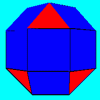
problemRhombicubocts
Each of these solids is made up with 3 squares and a triangle around each vertex. Each has a total of 18 square faces and 8 faces that are equilateral triangles. How many faces, edges and vertices does each solid have? -
 problem
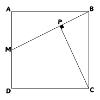
problemTwo Triangles in a Square
Given that ABCD is a square, M is the mid point of AD and CP is perpendicular to MB with P on MB, prove DP = DC. -
 problem
problemSliced
An irregular tetrahedron has two opposite sides the same length a and the line joining their midpoints is perpendicular to these two edges and is of length b. What is the volume of the tetrahedron? -
-
 problem
problemOne Reflection Implies Another
When a strip has vertical symmetry there always seems to be a second place where a mirror line could go. Perhaps you can find a design that has only one mirror line across it. Or, if you thought that was impossible, could you explain why ? -
-
 problem
problemEncircling
An equilateral triangle is sitting on top of a square. What is the radius of the circle that circumscribes this shape? -
 problem
problemSquare Pizza
Can you show that you can share a square pizza equally between two people by cutting it four times using vertical, horizontal and diagonal cuts through any point inside the square?
