Sine, cosine, tangent
-
-
 problem
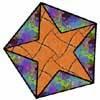
problemAt a glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it? -
 problem
problemFrom all corners
Straight lines are drawn from each corner of a square to the mid points of the opposite sides. Express the area of the octagon that is formed at the centre as a fraction of the area of the square. -
 problem
problemCircumnavigation
The sides of a triangle are 25, 39 and 40 units of length. Find the diameter of the circumscribed circle. -
 problem
problemThe dodecahedron
What are the shortest distances between the centres of opposite faces of a regular solid dodecahedron on the surface and through the middle of the dodecahedron? -
 problem
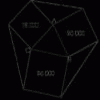
problemSqu-areas
Three squares are drawn on the sides of a triangle ABC. Their areas are respectively 18 000, 20 000 and 26 000 square centimetres. If the outer vertices of the squares are joined, three more triangular areas are enclosed. What is the area of this convex hexagon? -
-
 problem
problemFigure of eight
On a nine-point pegboard a band is stretched over 4 pegs in a "figure of 8" arrangement. How many different "figure of 8" arrangements can be made ? -
 problem
problemOrbiting billiard balls
What angle is needed for a ball to do a circuit of the billiard table and then pass through its original position? -
 problem
problemSpokes
Draw three equal line segments in a unit circle to divide the circle into four parts of equal area.
