Lying and cheating
Problem
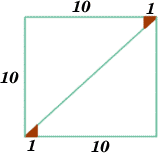
Follow the instructions and you can take a rectangle, cut it into 4 pieces, discard two small triangles, put together the remaining two pieces and end up with a rectangle the same size. Try it! Clearly there is something wrong here but can you explain what it is?
![]()
![]()
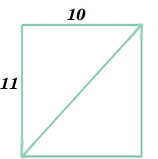
Take some squared paper and cut out a rectangle 10 units by 11 units. As shown in the diagram, cut along the diagonal and cut off the two red triangles, each of which has a side of length one unit. Put the two red triangles to one side.
Now slide the right hand piece down (moving one edge that had been the diagonal along the other) until you make another rectangle. The top edge of the new rectangle is 10 units long but the left hand edge becomes 11 units. Thus the new rectangle is the same as the one you started with. (11 units by 10 units).
Student Solutions
Sheila Luk (Year 10, The Mount School, York) saw right through this 'deception' and gave an excellent explanation of the situation.
The cheat is that although each triangle has a side of length 1 cm, the side at right angles to it is of length 10/ 11 cm. The diagonal of the rectangle does not go through the corners of the squares if it's drawn on squared paper.
The new rectangle, shown dotted, is not 11 by 10, but 10 10/ 11 by 10 and the difference in area is exactly 10/ 11 square cm, the area of the two triangles which were removed.
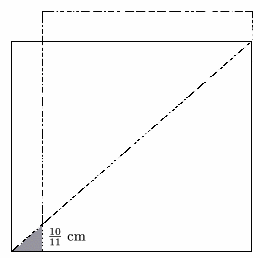
10 10/ 11 x 10 = 109 1/ 11= 110 - 10/ 11
Teachers' Resources
This problem is a good starter for lessons on gradients or the tangent function.
