problem
Reach 100
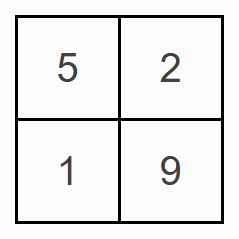
Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.

Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.

The large rectangle is divided into a series of smaller quadrilaterals and triangles. Can you untangle what fractional part is represented by each of the shapes?