Do you agree with Badger's statements? Is Badger's reasoning 'watertight'? Why or why not?
Ayah conjectures that the diagonals of a square meet at right angles. Do you agree? How could you find out?
Here is an interesting property about two sets of digits. Can you work out what the digits might be?
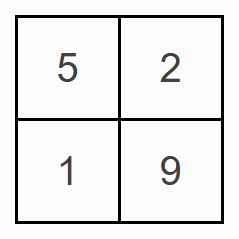
Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.
This practical problem challenges you to make quadrilaterals with a loop of string. You'll need some friends to help!
Find the product of the numbers on the routes from A to B. Which route has the smallest product? Which the largest?
