Number bases

problem
Back to basics

Age

14 to 16

Challenge level

Find b where 3723(base 10) = 123(base b).
problem
Phew I'm factored

Age

14 to 16

Challenge level

Explore the factors of the numbers which are written as 10101 in different number bases. Prove that the numbers 10201, 11011 and 10101 are composite in any base.
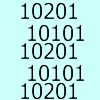problem
Composite notions

Age

14 to 16

Challenge level

A composite number is one that is neither prime nor 1. Show that 10201 is composite in any base.
problem
Fingers and hands

Age

7 to 11

Challenge level

How would you count the number of fingers in these pictures?
problem
It must be 2000

Age

7 to 11

Challenge level

Here are many ideas for you to investigate - all linked with the number 2000.
problem
Sometimes we lose things

Age

7 to 11

Challenge level

Well now, what would happen if we lost all the nines in our number system? Have a go at writing the numbers out in this way and have a look at the multiplications table.
game

Nim-like games

Age

7 to 16

Challenge level

A collection of games on the NIM theme
problem
Basically

Age

11 to 14

Challenge level

The number 3723 (in base 10) is written as 123 in another base. What is that base?
problem
Oh for the mathematics of yesteryear

Age

11 to 14

Challenge level

A garrison of 600 men has just enough bread ... but, with the news that the enemy was planning an attack... How many ounces of bread a day must each man in the garrison be allowed, to hold out 45 days against the siege of the enemy?
problem
Back to the planet of Vuvv

Age

11 to 14

Challenge level

There are two forms of counting on Vuvv - Zios count in base 3 and Zepts count in base 7. Can you work out in which direction the Zios and Zepts were looking, based on the information you're given?