Composite Notions
A composite number is one that is neither prime nor 1. Show that 10201 is composite in any base.
Problem
A composite number is one that is neither prime nor 1.
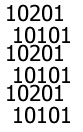
Show that 10201 is composite in any base.
Likewise show that 10101 is composite in any base.
Further Reading: Learn About Number Bases by Toni Beardon
Getting Started
The number 2356 in base 10 can be written
$ 2 \times 10^3 + 3 \times 10^2 + 5 \times 10^1 + 6 \times 10^0 = 2000 + 300 + 50 + 6$
So the number 234561 in base y can be written $2 \times y^5 + 3 \times y^4 + 4\times y^3 + 5 \times y^2 + 6 \times y^1 + 1 \times y^0$
How about factorising?
Student Solutions
The following solution was recieved from Andrei of School 205 Bucharest. Well done and thank you Andrei.
Therefore both expressions can be factorised, so they are composite.