Exploring and noticing
-

-
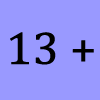 problemFavourite
problemFavouriteWhat could it be?
In this calculation, the box represents a missing digit. What could the digit be? What would the solution be in each case?
-
 problemFavourite
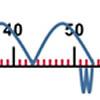
problemFavouriteFive steps to 50
Use five steps to count forwards or backwards in 1s or 10s to get to 50. What strategies did you use?
-
 problemFavourite
problemFavouriteSubtraction slip
Can you spot the mistake in this video? How would you work out the answer to this calculation?
-
 problemFavourite
problemFavouriteArranging additions and sorting subtractions
Order these four calculations from easiest to hardest. How did you decide?
-
 problem
problemStarfish spotting
How many starfish could there be on the beach, and how many children, if I can see 28 arms?
-
 problem
problemAmazing alphabet maze
Can you go from A to Z right through the alphabet in the hexagonal maze? -
 problemFavourite
problemFavouriteChain of changes
In this activity, shapes can be arranged by changing either the colour or the shape each time. Can you find a way to do it?
-
 problemFavourite
problemFavouriteMissing middles
Can you work out the domino pieces which would go in the middle in each case to complete the pattern of these eight sets of three dominoes?
-
 problemFavourite
problemFavouriteMaking sticks
Kimie and Sebastian were making sticks from interlocking cubes and lining them up. Can they make their lines the same length? Can they make any other lines?
