Prison cells
Problem
There are seventy eight prisoners in a square cell block of twelve cells. There is one prisoner in one of the cells, two in another cell, three in another, four in another and so on up to twelve prisoners in one of the cells.
The clever prison warder made it easy to check if the prisoners were all there by arranging them so there were twenty five along each wall of the prison block. How did he do it?
(There's more than one solution - send yours in - it might be different to everyone else's!)
Getting Started
What does this tell you about the total number of prisoners in the corner cells?
Student Solutions
Harriet sent in this solution. Well done!
She has explained her method in the middle of the grid.
Can you see how she did it?
Is this the only solution using her method?
Early in 2015 we had a solution from Ciaran and Alfie in year 5 at Petts Hill Primary In the U.K.
Thank you for this latest solution and the way it was illustrated.
At the beginning of 2016 we had two more solutions. These came from Collaton St. Mary School
Finley and Charlie sent in the first and Archie, Harrison, Huw and Younes sent in the second one.
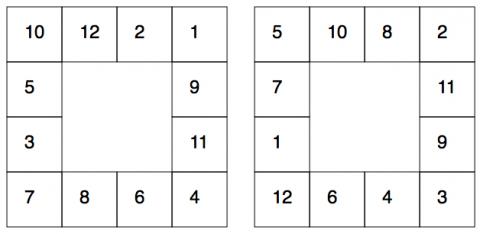
Thank you very much for these. Gavin from Hukanui Primary School in New Zealand also found the solution above on the left. Well done, Gavin!
Year 3 at Saint Patrick's Primary in Sunderland who worked together to find a solution:
1 11 3 10
12 9
5 2
7 8 6 4
Lew soon realised that you could switch the middle digits around and the totals wouldn't change e.g.
1 3 11 10
12 9
5 2
7 8 6 4
Then he noticed that this could be done systematically one at a time, for each pair of middle digits to find even more solutions. We call them "switch-its".
Following this, Connie realised that you could also swap whole rows or columns, e.g.
7 8 6 4
12 9
5 2
1 11 3 10
Therefore there are many different solutions using the same four numbers in the corners (7, 4, 1 and 10).
Thank you Sunderland for your good work!
Teachers' Resources
Prison Cells
There are seventy eight prisoners in a square cell block of twelve cells. There is one prisoner in one of the cells, two in another cell, three in another, four in another and so on up to twelve prisoners in one of the cells.
The clever prison warder made it easy to check if the prisoners were all there by arranging them so there were twenty five along each wall of the prison block. How did he do it?
(There's more than one solution - send yours in - it might be different to everyone else's!)
Why do this problem?
Possible approach
Key questions
What have we got to find out?
What do we know?
Possible extension
Children who find one solution quickly could be encouraged to find another one by rearranging some of the numbers in their own solution, rather than beginning afresh. In doing so they are beginning to generalise, an important mathematical skill. If you ask the children to record each solution on a separate piece of paper, then by moving and rearranging them they can see there are 'families' of solutions.
Possible support
Children who find this difficult could be given the grid with the corners filled in so that they start at a different place but end up with a complete solution, as everyone else.