Differentiation
-

-
 problem
problemBend
What is the longest stick that can be carried horizontally along a narrow corridor and around a right-angled bend? -
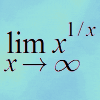 problem
problemExponential trend
Find all the turning points of y=x^{1/x} for x>0 and decide whether each is a maximum or minimum. Give a sketch of the graph. -
 problem
problemSlide
This function involves absolute values. To find the slope on the slide use different equations to define the function in different parts of its domain. -
 problem
problemQuick route
What is the quickest route across a ploughed field when your speed around the edge is greater? -
 problem
problemBird-brained
How many eggs should a bird lay to maximise the number of chicks that will hatch? An introduction to optimisation. -
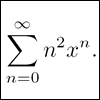 problem
problemGenerally geometric
Generalise the sum of a GP by using derivatives to make the coefficients into powers of the natural numbers. -

-
 problem
problemImpedance can be complex!
Put your complex numbers and calculus to the test with this impedance calculation. -
 problem
problemLeast of all
A point moves on a line segment. A function depends on the position of the point. Where do you expect the point to be for a minimum of this function to occur.
