Conjecturing and generalising

problem
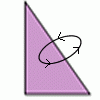In a spin

Age

14 to 16

Challenge level

What is the volume of the solid formed by rotating this right angled triangle about the hypotenuse?
problem
Overlap

Age

14 to 16

Challenge level

A red square and a blue square overlap. Is the area of the overlap always the same?
problem
Semi-square

Age

14 to 16

Challenge level

What is the ratio of the area of a square inscribed in a semicircle to the area of the square inscribed in the entire circle?
problem
Square pizza

Age

14 to 16

Challenge level

Can you show that you can share a square pizza equally between two people by cutting it four times using vertical, horizontal and diagonal cuts through any point inside the square?
problem
A tilted square

Age

14 to 16

Challenge level

The opposite vertices of a square have coordinates (a,b) and (c,d). What are the coordinates of the other vertices?
problem
Thank your lucky stars

Age

14 to 16

Challenge level

A counter is placed in the bottom right hand corner of a grid. You toss a coin and move the star according to the following rules: ... What is the probability that you end up in the top left-hand corner of the grid?
problem
Great Granddad

Age

11 to 14

Challenge level

Great Granddad is very proud of his telegram from the Queen congratulating him on his hundredth birthday and he has friends who are even older than he is... When was he born?
problem
Blue and white

Age

11 to 14

Challenge level

Identical squares of side one unit contain some circles shaded blue. In which of the four examples is the shaded area greatest?
problem
One o five

Age

11 to 14

Challenge level

You can work out the number someone else is thinking of as follows. Ask a friend to think of any natural number less than 100. Then ask them to tell you the remainders when this number is divided by 3, 5 and by 7...
problem
Chocolate maths

Age

11 to 14

Challenge level

Pick the number of times a week that you eat chocolate. This number must be more than one but less than ten. Multiply this number by 2. Add 5 (for Sunday). Multiply by 50... Can you explain why it works?