Conjecturing and generalising
-
 problemEqual touching circles have centres on a line. From a point of this line on a circle, a tangent is drawn to the farthest circle. Find the lengths of chords where the line cuts the other circles.
problemEqual touching circles have centres on a line. From a point of this line on a circle, a tangent is drawn to the farthest circle. Find the lengths of chords where the line cuts the other circles. -
 problem
problemMake 37
Four bags contain a large number of 1s, 3s, 5s and 7s. Can you pick any ten numbers from the bags so that their total is 37?
-
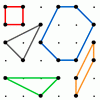 problem
problemPick's theorem
Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Find a relationship between p, i and the area of the polygons.
-
 problem
problemTake three from five
Caroline and James pick sets of five numbers. Charlie tries to find three that add together to make a multiple of three. Can they stop him?
-
 problem
problemThree times seven
A three digit number abc is always divisible by 7 when 2a+3b+c is divisible by 7. Why? -
 problem
problemHidden rectangles
Rectangles are considered different if they vary in size or have different locations. How many different rectangles can be drawn on a chessboard? -
 problem
problemThreesomes
Imagine an infinitely large sheet of square dotty paper on which you can draw triangles of any size you wish (providing each vertex is on a dot). What areas is it/is it not possible to draw? -
 problem
problemWhich is quicker?
Which is quicker, counting up to 30 in ones or counting up to 300 in tens? Why?
-

-
 problem
problemGot it
A game for two people, or play online. Given a target number, say 23, and a range of numbers to choose from, say 1-4, players take it in turns to add to the running total to hit their target.
