Overlap
A red square and a blue square overlap. Is the area of the overlap always the same?
Problem
A red square and a blue square of the same size are overlapping so that the corner of the red square rests on the centre of the blue square. Try using the slider to see how the overlap changes as the red square rotates.
Can you show that, whatever the orientation of the red square, it covers a quarter of the blue square?
Here are some ideas that you can use to help you do this:
This picture shows what happens if you rotate the red square by $90^{\circ}$, $180^{\circ}$ and $270^{\circ}$ around the centre of the blue square.

Can you use congurent triangles to complete this proof?

Can you use congruent triangles again to find a different proof?
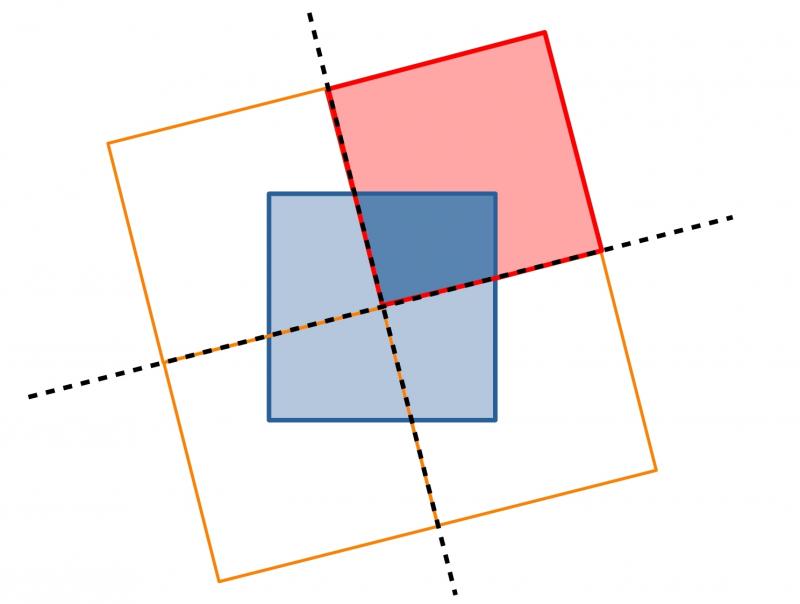
In this method, let each side of the blue square have length $2s$.
Can you use this diagram, and the areas of rectangles and triangles, to find a fourth proof?
If the red square is smaller than the blue square what is the smallest length its side can have for your proof to remain true?
Getting Started
Student Solutions
Well done to Tharuka from Doha College in Qatar, who sent in this solution:
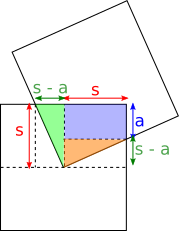
The way I will solve the first part of this question is by splitting each part into triangles and rectangles, like below:
Throughout the question, I will be using the terms a, b, x and y to describe each important part: orange = A; dark red = B, green = x, yellow = y.
The first part states that no matter the orientation, the red square will always take up a quarter of the blue square. I can prove this by using congruent triangles. Triangle A and B have the length of half of the blue square. Triangle A, and the area left behind in triangle B are congruent, so if you were to place the area of triangle A into the space left behind in triangle B, since the length of each triangle is half of the square, you would be able to see that the overlap is clearly the quarter of the blue square. That sounds convoluted but its really as simple as just placing the orange triangle in the dark red triangle.
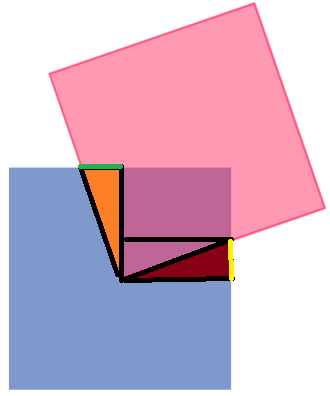
But how can we make sure that those two triangles are congruent, well let’s turn this diagram into something extremely simple. Look below:
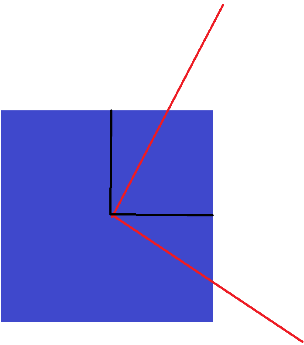
The two red lines are the sides of the red square. We can use the two black lines to check the distance each line moves. The two red lines are at a 90-degree angle, so as one rotates and moves, the other will move the same distance, meaning that the triangles made will have the same sides of their respective triangles and is thus congruent. For some final proof, here is a video of a program I made which shows further proof that triangle a and b are congruent by measuring the size of the line x and y (it’s not 100% accurate but it gets the point across):
Part 2
In this part of the question, I will prove that the red square must be over half the length of the blue square before the area of the overlap is smaller than a quarter of the blue square. Once again, I will use a diagram to explain this idea:
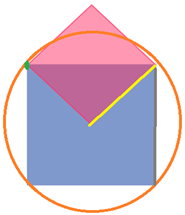
The green dot is a corner on the red square, the orange line is its orbit, the yellow line is x which is the length of the red square, and the grey line is y which is the length of the blue square.
As you can see here, the area of the overlap is the quarter of the blue square. This is because the green dot is outside/bordering the blue line. This means that the orbit is also outside the square. As the red square gets smaller, the orbit gets closer, and so does the green dot. Eventually, the circle and point will intersect the blue square, and as a result the overlap is less than a quarter of the blue square. This is because if we look at the part one of the question, once the points of the red square are inside the blue square, the area made between the edges and the center lines are quadrilaterals, that aren’t congruent and thus can’t be made into a quarter of a square.
So, the length of which the area of overlap is less than the quarter of the blue square is half of the blue square. The formula for this is x = 0.5y. This is because below this ratio of lengths, the point and orbit is within the blue square meaning that the area of the overlap is smaller than the quarter of the blue square.
This is excellent, except that in this case, $x$ is actually greater than $0.5y.$ Can you find the smallest possible value of $x$ in terms of $y$ (using Pythagoras' theorem)?
Teachers' Resources
Why do this problem?
This problem encourages students to appreciate that there can be more than one way to tackle a problem. The methods suggested here use symmetry, congruence, and areas. Each method has a picture which students are encouraged to use in order to complete a proof.
Possible approach
This problem featured in an NRICH Secondary webinar in March 2022.
Project the geogebra app onto a white board. Use the slider to rotate the red square around and ask students what fraction of the blue square they think is covered. In particular, look at when the red square is horizontal and when it makes an angle of $45^{\circ}$ with the horizontal. Do they think that the red square always covers the same fraction of the blue square?
There are 4 different proof methods to consider. You might find it helpful to provide students with a printout of the 4 pictures behind the "hide and reveal" buttons.
These printable worksheets could also be useful: Method 2, Method 3, Method 4. Each worksheet consists of a series of diagrams which form a proof, and space for students to add the explanations necessary to complete the proof.
