2D shapes and their properties
-

-
 problem
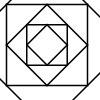
problemShaping it
These pictures were made by starting with a square, finding the half-way point on each side and joining those points up. You could investigate your own starting shape. -
 problem
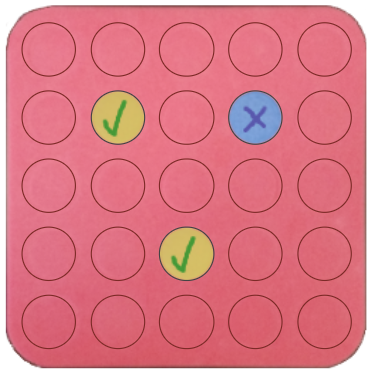
problemSeeing squares
Players take it in turns to choose a dot on the grid. The winner is the first to have four dots that can be joined to form a square.
-
 problem
problemPoly plug rectangles
The computer has made a rectangle and will tell you the number of spots it uses in total. Can you find out where the rectangle is?
-
 problem
problemAlways, sometimes or never? Shape
Are these statements always true, sometimes true or never true?
-

-
-
 problem
problemLet us reflect
Where can you put the mirror across the square so that you can still "see" the whole square? How many different positions are possible?
-
 problem
problemCircle panes
Look at the mathematics that is all around us - this circular window is a wonderful example. -
 problem
problemTorn shapes
These rectangles have been torn. How many squares did each one have inside it before it was ripped?
