2D shapes and their properties
-

-

-
 problem
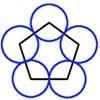
problemPolycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
-
 problem
problemCrescents and Triangles
Can you find a relationship between the area of the crescents and the area of the triangle?
-
 problem
problemBicentric Quadrilaterals
Investigate the properties of quadrilaterals which can be drawn with a circle just touching each side and another circle just touching each vertex. -
 problemFavourite
problemFavouriteBaby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
-
 problemFavourite
problemFavouriteLogosquares
Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.
-
 problem
problem2D-3D
Two circles of equal size intersect and the centre of each circle is on the circumference of the other. What is the area of the intersection? Now imagine that the diagram represents two spheres of equal volume with the centre of each sphere on the surface of the other. What is the volume of intersection?
-
 problem
problemBall Bearings
If a is the radius of the axle, b the radius of each ball-bearing, and c the radius of the hub, why does the number of ball bearings n determine the ratio c/a? Find a formula for c/a in terms of n.
-
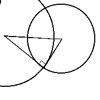 problemFavourite
problemFavouriteOrthogonal Circle
Given any three non intersecting circles in the plane find another circle or straight line which cuts all three circles orthogonally.
