Factorising with multilink
Can you find out what is special about the dimensions of rectangles you can make with squares, sticks and units?
How old am I?
In 15 years' time my age will be the square of my age 15 years ago. Can you work out my age, and when I had other special birthdays?
Beelines
Is there a relationship between the coordinates of the endpoints of a line and the number of grid squares it crosses?
Power countdown
In this twist on the well-known Countdown numbers game, use your knowledge of Powers and Roots to make a target.
Vector journeys
Charlie likes to go for walks around a square park, while Alison likes to cut across diagonally. Can you find relationships between the vectors they walk along?
Which list is which?
Six samples were taken from two distributions but they got muddled up. Can you work out which list is which?
Difference of two squares
What is special about the difference between squares of numbers adjacent to multiples of three?
Square number surprises
There are unexpected discoveries to be made about square numbers...
Triangle midpoints
You are only given the three midpoints of the sides of a triangle. How can you construct the original triangle?
Two ladders
Two ladders are propped up against facing walls. At what height do the ladders cross?
The spider and the fly
A spider is sitting in the middle of one of the smallest walls in a room and a fly is resting beside the window. What is the shortest distance the spider would have to crawl to catch the fly?
Where to land
Chris is enjoying a swim but needs to get back for lunch. How far along the bank should she land?
Matchless
There is a particular value of x, and a value of y to go with it, which make all five expressions equal in value. Can you find that x, y pair?
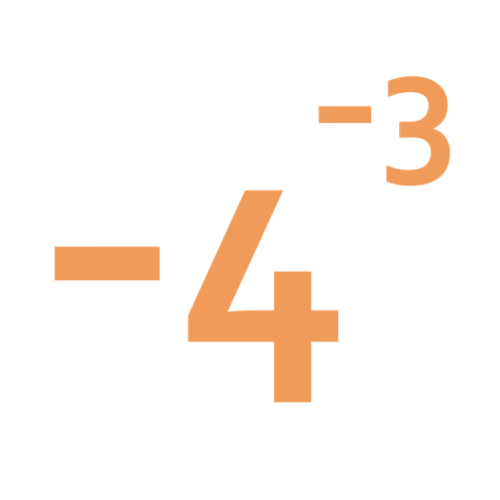
Negative powers
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
The legacy
Your school has been left a million pounds in the will of an ex- pupil. What model of investment and spending would you use in order to ensure the best return on the money?
Partly painted cube
Jo made a cube from some smaller cubes, painted some of the faces of the large cube, and then took it apart again. 45 small cubes had no paint on them at all. How many small cubes did Jo use?
Training schedule
The heptathlon is an athletics competition consisting of 7 events. Can you make sense of the scoring system in order to advise a heptathlete on the best way to reach her target?
Napkin
A napkin is folded so that a corner coincides with the midpoint of an opposite edge. Investigate the three triangles formed.
Dating made easier
If a sum invested gains 10% each year how long before it has doubled its value?
