Where to land
Problem
Chris is swimming in a lake, 50m from the shore.
Her family are 100m along the shore.
She'd like to get back to her family as quickly as possible. If she can swim at 3 m/sec and run at 7m/sec, how far along the shore should she land in order to get back as quickly as possible?
Getting Started
Try some particular landing points.
You might find a spreadsheet useful.
Student Solutions
We had a number of correct answers to this problem. Several solutions used a spreadsheet, for example the one shown below is from an anonymous solver. We also received a solution from someone who has done some calculus and was able to solve the problem using this approach. I have included this solution at the end for those of you who are interested.
My disappointment is that some of you are still just sending in answers without explanation and I do want to see how you arrived at your answers. Although the solution below was found using a spreadsheet you might have used a calculator and carried out a standard "trial and improvement" process to obtain the same result.
Catherine, Ellean, Anna from The Mount School, York add the following comment which means they were really thinking about the numbers and the context...
How fast do you think you could run and swim in m/s?
Andisheh of Springfield School offered the following explanation (well done):
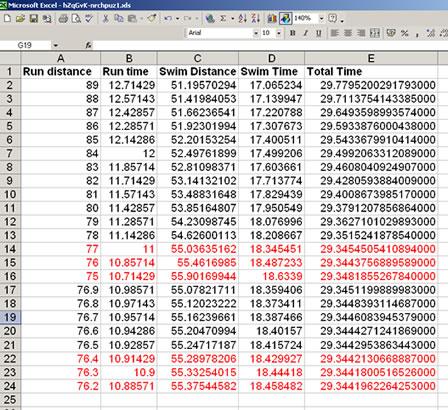
Andisheh attached a spreadsheet and I have used this and several other solutions employing a spreadhsheet to create the extract below: Solvers were able to find that the minimum time occurred with a distance between 76 and 77m and then worked with one and then two decimal places to obtain greater accuruacy.
"Swim Distance" was calculated using Pythagoras' theorem:The right-angled triangle will have sides of 50m (the distance from the beach) and $x$m, which is 100m (the distance along the beach) minus the distance run.
$$\mbox{Swim}^2 = 50^2 + x^2 $$
$$\mbox{Distance swum} = \sqrt{50^2 + x^2}$$
The times were then found in seconds by dividing the distances by the speeds and the total time just required the two times to be added.
The final solution was sent in by an anonymous solver who used calculus (a branch of mathematics normally met for the first time at advanced level in the UK). It is a neat solution but this high level mathematics was certainly not required!
Let $T$ be the total time.
Let $t_1$ be the time spent swimming.
Let $t_2$ be the time spent running.
By Pythagoras' theorem
\begin{eqnarray} PC^2 &=& 50^2 + x^2 \\ PC&=& \sqrt{50^2 + x^2} \end{eqnarray}
So for the total time:
$$ T = \frac{\sqrt{x^2 + 50^2}}{3} + \frac{100-x}{7}$$
$$\frac{dT}{dx} = \frac{x(x^2 + 50^2)^\frac{-1}{2}}{3}- \frac{1}{7}$$
$$\frac{dT}{dx} = 0 \mbox{ when } \frac{1}{7} = \frac{x(x^2 + 50^2)^\frac{-1}{2}}{3}$$ Important question to think about:
How would you check that this is a minimum value?
Solving the equation above for $x$
\begin{eqnarray} 3(x^2+50^2)^\frac{1}{2} &=& 7x\\ 9(x^2+50^2)&=& 49x^2\\ x&=& 23.7 \mbox{ (1dp)} \end{eqnarray}
Chris will need to land at the point on the beach 76.3m from the family.
Teachers' Resources
Why do this problem?
This problem requires students to apply Pythagoras’ Theorem in context. They will derive an expression to maximise rather than an equation to solve. There are opportunities for trial and error or drawing and interpreting graphs, and/or using graphing or spreadsheet software. Very advanced students might approach the problem using calculus.
The ideas in this problem can also be related to the bending of light rays as they meet a different substance.
Possible approach
You might start by displaying the graphic in the question and introducing the problem using the edge cases of minimum and/or maximum swimming. Students could then spend some time trying particular landing points. Some students may need to be reminded of the speed, distance, time equation and the relevant rearrangements. Combining the class’s results might be sufficient to find the best integer value.
You could compare methods all together at this point and generalise to find a ‘total time’ formula. You could use the formula to use a trial and improvement method like interval splitting, or spreadsheet software like Excel.
Alternatively, you could ask the students to graph their formula, either by hand or using graphing software they are familiar with. By hand, they could begin by plotting the integer points that they have already found. How do we interpret the graph to find our final solution? There is an opportunity here to discuss the level of accuracy we might expect from hand drawn graphs.
Key questions
How long does it take if Chris swims straight to the river bank?
If you choose a landing point, can you find how long the journey will take?
Can we use algebra to represent any landing point?
Is there a way to visualise lots of different possibilities for x all at once?
Possible support
Garden Shed offers practice using Pythagoras’ Theorem in a different context. A structured spreadsheet could be made that allowed students to enter distances and see a ‘total time’ output. This would shift the focus of the task toward effective use of trial and error.
Possible extension
What happens if you change the speeds Chris can swim and run?
Capable students might use calculus to solve the problem. Ladder and Cube also uses Pythagoras’ Theorem and could include elements of numerical analysis.
For a similar problem involving a circular swimming pool see To Swim or to Run?