
Standing, from left to right: Karen, Lisa, Stuart, Emma, Chris, Dana, Chad, Kim, Gohar, Gene, Sara, Ingrid, and Charlie, not standing
"I don't expect, and I don't want, all children to find mathematics an engrossing study, or one that they want to devote themselves to either in school or in their lives. Only a few will find mathematics seductive enough to sustain a long term engagement. But I would hope that all children could experience at a few moments in their careers ... the power and excitement of mathematics ... so that at the end of their formal education they at least know what it is like and whether it is an activity that has a place in their future."
David Wheeler
Key ideas that inform the work of NRICH
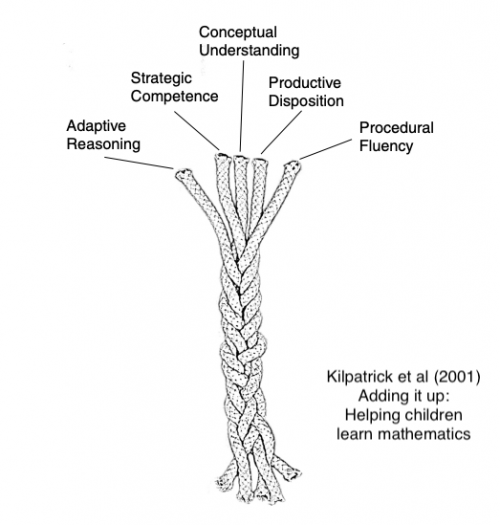
Nurturing Successful Mathematicians: the Rope Model
Alan Wigley's article on Models for Teaching Mathematics
An example of what this might look like in practice:
Tilted Squares and the recording of a lesson
Our guiding principles
Maths is for all
All have a right to shine, and all have a right to struggle
Low Threshold / High Ceiling tasks allow for differentiation
Allow time for exploration and discussion
Start with an engaging problem/context (Wigley article)
Tap into students' curiosity: "What questions are bubbling up for you?"
Offer students the opportunity to go on mathematical journeys
Exploring, noticing patterns, conjecturing, generalising, justifying, proving
Think-pair-share / Convince yourself, convince a friend, convince others...
Encourage multiple strategies / representations
We publish students' solutions
Value a Growth Mindset (Carol Dweck)
It’s ok to make mistakes - learning is a messy business
There’s always help at hand but we still expect students to do the thinking
Celebrate resourcefulness and resilience ("Yet")
To find out more, see What we think and why we think it
and Resources and Professional development
Links to resources to support Primary teachers:
Links to resources to support Secondary teachers:
- Secondary Curriculum
- Enriching the Secondary Curriculum
- Don Steward's resources
- Solving Together aims to promote parental engagement with mathematics
- Recommended books for young people who are interested in mathematics
Links to resources to support Post-16 teachers:
- Underground Mathematics
- RISPS - Rich Starting Points for A Level Mathematics
- NRICH Post-16 page
- STEP support programme
- Plus magazine
- Quanta magazine
Problems we worked on during the week:
The Number Jumbler
Summing consecutive numbers
Unequal Averages
Wipeout
Xavi's T-shirt
Cyclic Quadrilaterals
Generating triples
In this film (available here if you live outside the UK) the mathematician Andrew Wiles talks about his personal experience of seeking a proof of Fermat's Last Theorem.
Amazing Card Trick
Truth or Lie
Ace, two, three...
Matt Parker's favourite card trick
Some interactivities on the Secondary mapping document, and on the Secondary interactive resources page:
More less is more
Dozens
Square it
Fruity totals
Bringing everything together
Poster 1
Poster 2
Poster 3
Poster 4
Poster 5
Further recommendations
Peter Liljedahl's Building Thinking Classrooms
Colin Foster's Mathematical etudes
Productive Math Struggle
Productive Failure - Manu Kapur's 2019 Ted talk and book
NCTM's 5 Practices for Orchestrating Productive Mathematics Discussions
Henri Picciotto and Robin Pemantle's There is no one way to teach Math
Mathematica: A Secret World of Intuition and Curiosity by David Bessis, and a discussion about the book.
Mihaly Csikszentmihalyi's Flow
Yōko Ogawa's The Housekeeper and the Professor
Steven Strogatz's Infinite Powers: How Calculus Reveals the Secrets of the Universe
Matt Parker's Humble Pi
Arthur Benjamin and Michael Shermer's Secrets of Mental Math
Math Circles - connecting mathematicians of all ages
Teachers can Register for our monthly email newsletter to be kept up to date with our latest news.
"A teacher of mathematics has a great opportunity. If he fills his allotted time with drilling his students in routine operations he kills their interest, hampers their intellectual development, and misuses his opportunity. But if he challenges the curiosity of his students by setting them problems proportionate to their knowledge, and helps them to solve their problems with stimulating questions, he may give them a taste for, and some means of, independent thinking."
Polya, G. (1945) How to Solve it
