What is the greatest volume you can get for a rectangular (cuboid) parcel if the maximum combined length and girth are 2 metres?
My measurements have got all jumbled up! Swap them around and see if you can find a combination where every measurement is valid.
Here's a chance to work with large numbers...
Can you sketch graphs to show how the height of water changes in different containers as they are filled?
How can you change the surface area of a cuboid but keep its volume the same? How can you change the volume but keep the surface area the same?
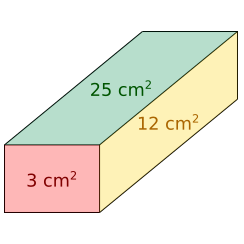
A box has faces with areas 3, 12 and 25 square centimetres. What is the volume of the box?
Use a single sheet of A4 paper and make a cylinder having the greatest possible volume. The cylinder must be closed off by a circle at each end.
An aluminium can contains 330 ml of cola. If the can's diameter is 6 cm what is the can's height?
What's the largest volume of box you can make from a square of paper?
