Making Boxes
In this problem you start with some sheets of squared paper measuring $15\times 15$ and use them to make little boxes without lids.
You do this by cutting out squares at the corners and then folding up the sides. (The folds are indicated by the dotted lines in the diagram.)
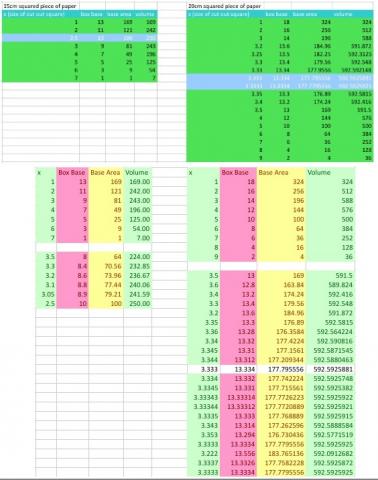
Begin by cutting one square out of each corner. Fold up the sides. What is the size of the base? How high are the sides? So what is its volume?
Now cut a $2 \times 2$ square out of each corner and fold up the sides.
Does it look as if it holds more than the first box, less than the first box or just the same amount?
What is the size of the base now? How high are the sides now? So what is its volume?
Now cut a $3 \times 3$ square out of each corner and fold up the sides.
Does it look as if it holds more than the other boxes, less than the other boxes or just the same amount?
What is the size of the base now? How high is it now? So what is its volume?
If you keep on doing this, taking larger and larger squares from the corners, which box will have the largest volume?
Why do this problem?
This activity could be used to extend learners' ideas about area. It is also a valuable activity for the introduction of volume, although it is quite possible to do the investigation without using the word. Learners can be asked to visualise the boxes they are about to make, and it may be that some pupils turn to visualisation as the main route to a solution. In addition, this problem is useful for practising multiplication tables, especially squares.
Possible approach
You could start by demonstrating making the lidless boxes from a $10 \times10$ square. First cut one square from each corner and fold up the edges.
Ask learners what the area of the base is and how many cubes it would hold. How do they know? Explain that you are going to cut a $2 \times2$ square from each corner next, but before doing so, ask the group to visualise the resulting box. What would the area of the base be this time and how many cubes would it hold? Either make the box for the children to see, or invite them to check their visualisations in pairs. Continue with a $3 \times3$ square cut from each corner but this time do not ask about the size, simply ask them to picture the box in their heads. (A $10 \times10$ square, which can be enlarged for a bigger group, can be downloaded
here.
)
Pose the problem itself and give learners squared paper (centimetre squares are ideal) to work on a solution in pairs so that they are able to talk through their ideas with a partner. You may like to encourage learners to predict which box will have the largest volume and to give a reason for their prediction. You will need to supply scissors and possibly sticky tape. Some might make a table of their results, or you could collate the class results on the board for everyone to see. Continuing with differently-sized squares, both smaller and larger than $15$, will produce some interesting number patterns.
In the plenary, invite learners to show their work and discuss the results. Were their predictions correct? What do they notice about the volume as the cut-out squares get bigger? Can they get a feel for why this is? A display of a series of boxes can be made with the different volumes written in the base.
Key questions
How big is the base/bottom of this box? How high are the sides? So how much does it hold?
Are you sure that this is a square? Why not count it and see?
What is happening to the volume as we cut bigger squares out of the paper?
Possible extension
Learners could make a graph of their results as well as trying differently-sized starting squares. Those who really do not need to make many boxes to make the calculations could try intermediate corner numbers such as $2.5 \times 2.5$ cut from the original square. Alternatively, they could try
this more advanced version of the problem.
Possible support
Some learners might find it easier to start with a $12 \times 12$ square. This means that the base of the first box is $10 \times10$, which gives a familiar starting number. You may also find centimetre cubes useful.