Visualising and representing
-

-
 problem
problemDoubly symmetric
What is the smallest number of additional squares that must be shaded so that this figure has at least one line of symmetry and rotational symmetry of order 2? -
 problem
problemTravelling by train
Stephen stops at Darlington on his way to Durham. At what time does he arrive at Durham? -
 problem
problemOldest and youngest
Edith had 9 children at 15 month intervals. If the oldest is now six times as old as the youngest, how old is her youngest child? -

-
 problem
problemSame face
A cube is rolled on a plane, landing on the squares in the order shown. Which two positions had the same face of the cube touching the surface? -
 problem
problemTennis training
After tennis training, Andy, Roger and Maria collect up the balls. Can you work out how many Andy collects? -

-
 problem
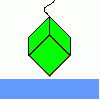
problemAll in the mind
Imagine you are suspending a cube from one vertex and allowing it to hang freely. What shape does the surface of the water make around the cube? -
 problem
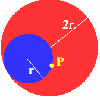
problemJust rolling round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
