Vector notation and geometry
-

-
 problemFavourite
problemFavouriteSpotting the Loophole
A visualisation problem in which you search for vectors which sum to zero from a jumble of arrows. Will your eyes be quicker than algebra?
-
 problemFavourite
problemFavouriteTriangle in a Triangle
Can you work out the fraction of the original triangle that is covered by the inner triangle?
-
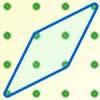 problemFavourite
problemFavouriteAreas of Parallelograms
Can you find the area of a parallelogram defined by two vectors?
-
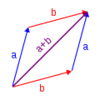 problemFavourite
problemFavouriteVector Walk
Starting with two basic vector steps, which destinations can you reach on a vector walk?
-
 problemFavourite
problemFavouriteVector Journeys
Charlie likes to go for walks around a square park, while Alison likes to cut across diagonally. Can you find relationships between the vectors they walk along?
-
 gameFavourite
gameFavouriteVector Gem Collector
Use vectors to collect as many gems as you can and bring them safely home!
-
 problemFavourite
problemFavouriteFlexi Quads
A quadrilateral changes shape with the edge lengths constant. Show the scalar product of the diagonals is constant. If the diagonals are perpendicular in one position are they always perpendicular?
-
 problemFavourite
problemFavouriteTetra Perp
Show that the edges $AD$ and $BC$ of a tetrahedron $ABCD$ are mutually perpendicular if and only if $AB^2 +CD^2 = AC^2+BD^2$. This problem uses the scalar product of two vectors.
-
 problem
problemSpiroflowers
Analyse these repeating patterns. Decide on the conditions for a periodic pattern to occur and when the pattern extends to infinity.
