Flexi Quads
A quadrilateral changes shape with the edge lengths constant. Show
the scalar product of the diagonals is constant. If the diagonals
are perpendicular in one position are they always perpendicular?
Age
16 to 18
Challenge level
Problem
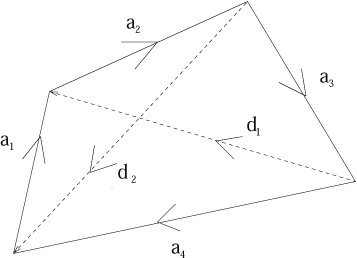
Consider a convex quadrilateral $Q$ made from four rigid rods with flexible joints at the vertices so that the shape of $Q$ can be changed while keeping the lengths of the sides constant. Let ${\bf a}_1$, ${\bf a}_2$, ${\bf a}_3$ and ${\bf a}_4$ be vectors representing the sides (in this order) of an arbitrary quadrilateral $Q$, so that ${\bf a}_1+{\bf a}_2+{\bf a}_3+{\bf a}_4 = {\bf 0}$ (the zero vector). Now let ${\bf d}_1$ and ${\bf d}_2$ be the vectors representing the diagonals of $Q$. We may choose these so that ${\bf d}_1={\bf a}_4+{\bf a}_1$ and ${\bf d}_2={\bf a}_3+{\bf a}_4$. Prove that
$${\bf a}_2^2+{\bf a}_4^2-{\bf a}_1^2-{\bf a}_3^2= 2({\bf a}_1{\cdot}{\bf a}_3-{\bf a}_2{\cdot}{\bf a}_4).\quad (1)$$
and that the scalar product of the diagonals is constant and given by:
$$2{\bf d}_1{\cdot}{\bf d}_2 = {\bf a}_2^2+{\bf a}_4^2-{\bf a}_1^2-{\bf a}_3^2.\quad (2)$$
Use these results to show that, as the shape of the quadrilateral is changed, if the diagonals of $Q$ are perpendicular in one position of $Q$, then they are perpendicular in all variations of $Q$.
Getting Started
Use the scalar product of the diagonals. As the quadrilateral is flexed the diagonals change but the lengths of the sides are constant. All the vectors change but the the squares of the vectors of the sides (representing the lengths) remain constant. To preserve symmetry and obtain this scalar product in the form required, write
$$2{\bf d}_1={\bf a}_1-{\bf a}_2-{\bf a}_3+{\bf a}_4, \quad 2{\bf d}_2=-{\bf a}_1-{\bf a}_2+{\bf a}_3+{\bf a}_4.$$
Student Solutions
This excellent solution came from Shu Cao of Oxford High School. Well done Shu!
Image
A convex quadrilateral $Q$ is made from four rigid rods with
flexible joints at the vertices so that the shape of $Q$ can be
changed while keeping the lengths of the sides constant.
Let ${\bf a}_1$, ${\bf a}_2$, ${\bf a}_3$ and ${\bf a}_4$ be
vectors representing the sides (in this order) so that ${\bf
a}_1+{\bf a}_2+{\bf a}_3+{\bf a}_4 = {\bf 0}$ (the zero vector).
Now let ${\bf d}_1$ and ${\bf d}_2$ be the vectors representing the
diagonals of $Q$. We may choose these so that ${\bf d}_1={\bf
a}_4+{\bf a}_1$ and ${\bf d}_2={\bf a}_3+{\bf a}_4$.
As ${\bf d}_1={\bf a}_4 + {\bf a}_1$ and ${\bf d}_2 = {\bf
a}_3 + {\bf a}_4$ it follows that ${\bf a}_1 + {\bf a}_2 = -{\bf
d}_2,\ {\bf a}_2 + {\bf a}_3 = -{\bf d}_1.$
$$\eqalign{ {\bf a}_2^2+{\bf a}_4^2-{\bf a}_1^2-{\bf a}_3^2
&=({\bf a}_2^2-{\bf a}_1^2)+({\bf a}_4^2-{\bf a}_3^2) \cr
&=({\bf a}_2-{\bf a}_1)({\bf a}_2+{\bf a}_1)+({\bf a}_4-{\bf
a}_3)({\bf a}_4+{\bf a}_3)\cr &=-{\bf d}_2({\bf a}_2-{\bf
a}_1)+{\bf d}_2({\bf a}_4-{\bf a}_3)\cr &={\bf d}_2({\bf
a}_4-{\bf a}_3-{\bf a}_2+{\bf a}_1)\cr &={\bf d}_2(({\bf
a}_4+{\bf a}_1)-({\bf a}_3+{\bf a}_2))\cr &={\bf d}_2({\bf
d}_1+{\bf d}_1)\cr &=2{\bf d}_2 {\bf .} {\bf d}_1 }.$$
Now ${\bf a}_1+{\bf a}_2+{\bf a}_3+{\bf a}_4=0$ implies that
${\bf a}_4=-{\bf a}_1-{\bf a}_2-{\bf a}_3$.
$$\eqalign{ {\bf a}_1 \cdot {\bf a}_3-{\bf a}_2 {\bf .} {\bf
a}_4 &= {\bf a}_1 {\bf .} {\bf a}_3-{\bf a}_2(-{\bf a}_1-{\bf
a}_2-{\bf a}_3) \cr &={\bf a}_1 {\bf .} {\bf a}_3+{\bf a}_2
{\bf .} {\bf a}_1+{\bf a}_2{\bf .} {\bf a}_2+{\bf a}_2{\bf .} {\bf
a}_3 \cr &={\bf a}_1({\bf a}_2+{\bf a}_3)+{\bf a}_2({\bf
a}_2+{\bf a}_3) \cr &=({\bf a}_1+{\bf a}_2)({\bf a}_3+{\bf
a}_2) \cr &=(-{\bf d}_1)(-{\bf d}_2) \cr &={\bf d}_1{\bf .}
{\bf d}_2}.$$
Hence
$$\eqalign{ 2({\bf a}_1 {\bf .} {\bf a}_3-{\bf a}_2 {\bf .}
{\bf a}_4) &=2{\bf d}_1 {\bf .} {\bf d}_2 \cr &={\bf
a}_2^2+{\bf a}_4^2-{\bf a}_1^2-{\bf a}_3^2 .}$$
If the diagonals of $Q$ are perpendicular in one position of
$Q$, then $2{\bf d}_1 {\bf .} {\bf d}_2={\bf a}_2^2+{\bf
a}_4^2-{\bf a}_1^2-{\bf a}_3^2 =0$. As ${\bf a}_1,{\bf a}_2,{\bf
a}_3,{\bf a}_4$ are constant in length ${\bf a}_2^2+{\bf
a}_4^2-{\bf a}_1^2-{\bf a}_3^2$ will always be zero which implies
that ${\bf d}_1 {\bf .} {\bf d}_2=0$, so they are perpendicular in
all variations of $Q$.