Symmetry

article
The Frieze Tree

Patterns that repeat in a line are strangely interesting. How many types are there and how do you tell one type from another?
problem

Classifying Solids Using Angle Deficiency

Age

11 to 16

Challenge level

Toni Beardon has chosen this article introducing a rich area for practical exploration and discovery in 3D geometry
problem

Trominoes

Age

11 to 16

Challenge level

Can all but one square of an 8 by 8 Chessboard be covered by Trominoes?
problem
Favourite

Arclets

Age

14 to 16

Challenge level

Each of the following shapes is made from arcs of a circle of radius r. What is the perimeter of a shape with 3, 4, 5 and n "nodes".
problem

Overlap

Age

14 to 16

Challenge level

A red square and a blue square overlap. Is the area of the overlap always the same?
problem
Favourite

Attractive Tablecloths

Age

14 to 16

Challenge level

Charlie likes tablecloths that use as many colours as possible, but insists that his tablecloths have some symmetry. Can you work out how many colours he needs for different tablecloth designs?
problem

A Problem of Time

Age

14 to 16

Challenge level

Consider a watch face which has identical hands and identical marks for the hours. It is opposite to a mirror. When is the time as read direct and in the mirror exactly the same between 6 and 7?
problem
Favourite

Logosquares

Age

16 to 18

Challenge level

Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.
problem
Favourite

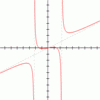
Witch of Agnesi

Age

16 to 18

Challenge level

Sketch the members of the family of graphs given by $y = a^3/(x^2+a^2)$ for $a=1, 2$ and $3$.
problem

Dicey Decisions

Age

16 to 18

Challenge level

Can you devise a fair scoring system when dice land edge-up or corner-up?