Dancing with Maths

• A snowflake
• A starfish
• A butterfly

They all have symmetry.

Symmetry is the basis of all patterns in art, music, bell ringing, knitting, dancing, crystals, elementary particles and nature.

Reflection	Rotation	Translation
Image	Image	Image

Something is said to be symmetric if it is not changed by one or more of these operations (reflection, rotation or translation).

Lots of art is based on symmetry, here is a very old example:

Image

Squares

A square is symmetric. How many symmetries does it have?

A square will look the same under any combination of these symmetries but if we label the corners of the square and apply rotations and reflections we end up with "different" squares. Here are four examples (I have named them 'a', 'b', 'c' and 'd'.

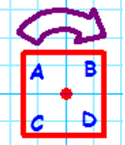
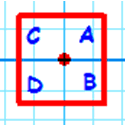
Rotation	Image	Image	Image	a
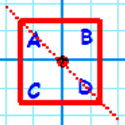
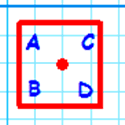
Reflection	Image	Image	Image	b
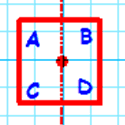
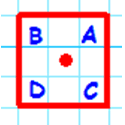
Reflection	Image	Image	Image	c
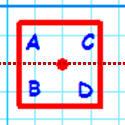
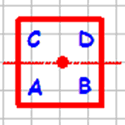
Reflection	Image	Image	Image	d

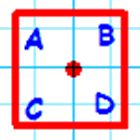
The simplest symmetry we can have is the"do nothing "symmetry which we shall call 'e'.

Image	Image		Image
	We call this symmetry	e

We can combine these symmetries to get new ones.

So, for example:

You can also combine reflections with themselves:

Answers are at the end of this article.

We have looked at combining rotations and combining reflections but what happens if we combine a rotation with a reflection? Let's look.

Reflection and rotation: ba = ?

Image

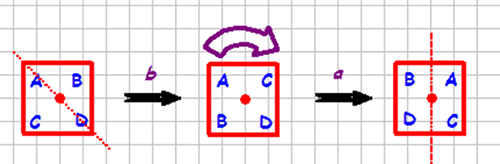
Reflection and rotation ba = ?

So - how about ab?

Image

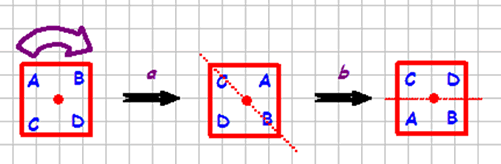
And how about two reflections? bc = ?

Image

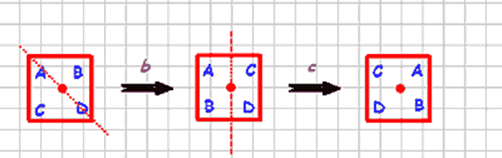
Answers are at the end of the article.

Here are some other combinations you might like to check for yourself:

By now you might be asking yourself:

"What has all this got to do with dancing?".

Well let me explain...

My name is Chris and fortunately I have three friends called Andrew, Bryony and Daphne (that makes A, B, C and D) who all like dancing.

Image

We make ABCD - four corners of a square. You might already be seeing the connection! If not, here's a hint:

Image

Key Fact: the symmetries of the square correspond to different dance moves.

Reflection

Image

Image

Image

b

Dance move

ABCD

Image

ACBD

This dance move is called an "inner-twiddle " or "dos-e-dos "

Reflection

Image

Image

Image

c

Dance move

ABCD

Image

BADC

This dance move is called an "outer-twiddle " or "Swing "

Now for the clever bit:

And this coresponds to a dance called a "Reel of Fou r " or a "Hey ".

Let's do the dance

		ABCD
b	Image
		ACBD
c	Image
		CADB
b	Image
		CDAB
c	Image
		DCBA
b	Image
		DBCA
c	Image
		BDAC
b	Image
		BADC
c	Image
		ABCD

Now find three friends and try it!

Another dance

ABCD	Image	CDAB
	d b = a

Therefore

d b d b d b d b = aaaa = e

		ABCD
d	Image
		CDAB
b	Image
		CADB
d	Image
		DBCA
b	Image
		DCBA
d	Image
		BADC
b	Image
		BDAC
d	Image
		ACBD
b	Image
		ABCD

We see the same patterms in bell ringing and in knitting.

Why not see whether you can find other places?

Answers

A square has 8 symmetries; 4 rotation symmetries and 4 reflection symmetries

bb, cc and dd all equal e.

ba = c

ab = d

bc = a