Rational and irrational numbers
-

-
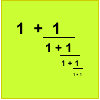 article
articleContinued fractions II
In this article we show that every whole number can be written as a continued fraction of the form k/(1+k/(1+k/...)).
-
 article
articleApproximations, Euclid's algorithm and continued fractions
This article sets some puzzles and describes how Euclid's algorithm and continued fractions are related.
-
 article
articleAll is number
Read all about Pythagoras' mathematical discoveries in this article written for students.
-
 article
articleThe dangerous ratio
This article for pupils and teachers looks at a number that even the great mathematician, Pythagoras, found terrifying. -
 article
articleAn introduction to proof by contradiction
An introduction to proof by contradiction, a powerful method of mathematical proof. -
 article
articleWhat are numbers?
Ranging from kindergarten mathematics to the fringe of research this informal article paints the big picture of number in a non technical way suitable for primary teachers and older students. -
 interactivity
interactivityProof sorter - the square root of 2 is irrational
Try this interactivity to familiarise yourself with the proof that the square root of 2 is irrational. Sort the steps of the proof into the correct order. -
 problem
problemGood approximations
Solve quadratic equations and use continued fractions to find rational approximations to irrational numbers. -
 problem
problemBe reasonable
Prove that sqrt2, sqrt3 and sqrt5 cannot be terms of ANY arithmetic progression.
