Powers and roots
-

-
 problem
problemGuesswork
Ask a friend to choose a number between 1 and 63. By identifying which of the six cards contains the number they are thinking of it is easy to tell them what the number is.
-
 problem
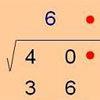
problemUnusual long division - square roots before calculators
However did we manage before calculators? Is there an efficient way to do a square root if you have to do the work yourself? -

-

-
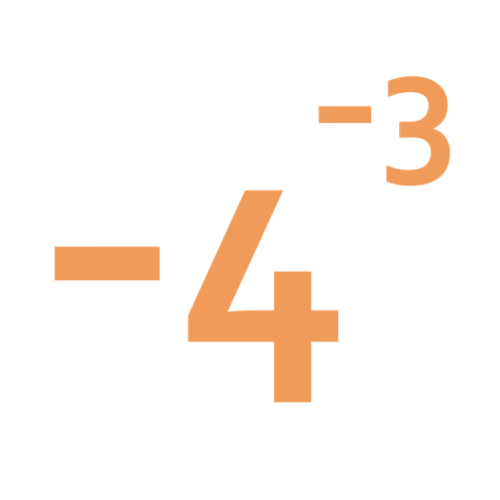 problem
problemNegative powers
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
-
 problem
problemArchimedes numerical roots
How did Archimedes calculate the lengths of the sides of the polygons which needed him to be able to calculate square roots?
-
 problem
problemFunction pyramids
A function pyramid is a structure where each entry in the pyramid is determined by the two entries below it. Can you figure out how the pyramid is generated?
-

-

