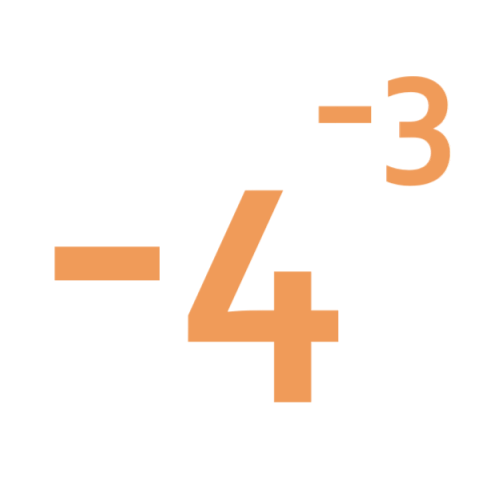
problem
Favourite
Negative Powers
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
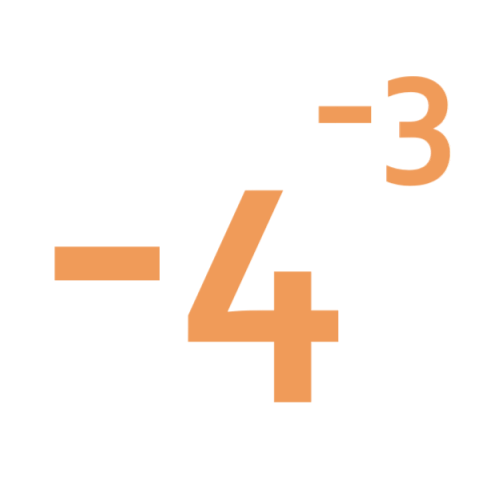
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?
Which is the biggest and which the smallest of $2000^{2002}, 2001^{2001} \text{and } 2002^{2000}$?
Can you prove that twice the sum of two squares always gives the sum of two squares?
Find $S_r = 1^r + 2^r + 3^r + ... + n^r$ where r is any fixed positive integer in terms of $S_1, S_2, ... S_{r-1}$.
Which is the bigger, 9^10 or 10^9 ? Which is the bigger, 99^100 or 100^99 ?