Groups

problem

Rose

Age

16 to 18

Challenge level

What groups of transformations map a regular pentagon to itself?
problem

What's a Group?

Age

16 to 18

Challenge level

Explore the properties of some groups such as: The set of all real numbers excluding -1 together with the operation x*y = xy + x + y. Find the identity and the inverse of the element x.
problem

Groups of Sets

Age

16 to 18

Challenge level

The binary operation * for combining sets is defined as the union of two sets minus their intersection. Prove the set of all subsets of a set S together with the binary operation * forms a group.
problem

Simplifying Transformations

Age

11 to 14

Challenge level

How many different transformations can you find made up from combinations of R, S and their inverses? Can you be sure that you have found them all?
problem

Sheep in Wolf's Clothing

Age

16 to 18

Challenge level

Can you work out what simple structures have been dressed up in these advanced mathematical representations?
article
Small Groups

Learn about the rules for a group and the different groups of 4 elements by doing some simple puzzles.
article
An Introduction to Mathematical Structure

An introduction to the sort of algebra studied at university, focussing on groups.
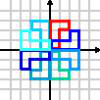
article
Grouping Transformations

An introduction to groups using transformations, following on from the October 2006 Stage 3 problems.
article
Dancing With Maths

An article for students and teachers on symmetry and square dancing. What do the symmetries of the square have to do with a dos-e-dos or a swing? Find out more?
article
Paint Rollers for Frieze Patterns

Proofs that there are only seven frieze patterns involve complicated group theory. The symmetries of a cylinder provide an easier approach.