Rose
What groups of transformations map a regular pentagon to itself?
Problem
|
1
Image

|
2 Image
|
3 Image
|
4 Image

|
|
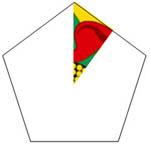
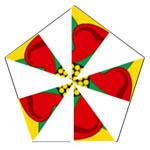
List the symmetries in each of the four diagrams, that is the
transformations which map the picture into itself.
What transformations do you get if you combine the
transformations from diagrams 3 and 4 in all possible ways?
A set of transformations, with the operation of combining
transformations, becomes a group when the set includes all possible
combinations of the transformations in the set.
Do the sets of transformations you have listed form groups
when their transformations are combined?
Can you find any other groups of transformations which map a
regular pentagon to itself?
How many distinctly different groups are there which map a
regular pentagon into itself?
Note: You don't need to do
more in order to submit a solution but why not pose some similar
questions for yourself? The article Paint Rollers for Frieze Patterns
explores in 3D the same idea of
groups of symmetries.
|
Getting Started
There are four cases to consider:
(a) the group containing only the identity transformation
(b) groups containing the identity and rotations
(c) groups containing the identity and reflections
(d) groups containing the identity, reflections and rotations.
(a) the group containing only the identity transformation
(b) groups containing the identity and rotations
(c) groups containing the identity and reflections
(d) groups containing the identity, reflections and rotations.
Teachers' Resources
Why do this problem?
Groups play a key role in understanding the underlying patterns in geometric art as well as underpinning arithmetic, algebra, geometry and being useful in many applications of mathematics.
This challenge is structured to enable learners to find out for themselves about the group of symmetries of a regular pentagon and to find all of its subgroups.They don't have to have any prior knowledge of groups and they do not need to know the axioms of a group because with transformations there is always an inverse. They only need to know that they are looking for sets of transformations which are closed under the operation of taking combinations.
Possible approach
The class could start by listing the symmetries in the four diagrams and discussing how to use symbols for the transformations. Class discussion can then explore the key ideas:
(1) a combination of two reflections in intersecting lines gives a rotation and so once a group contains two reflections it must contain all the symmetries of the pentagon
(2) a group that contains a reflection and a rotation contains all the symmetries of the pentagon
You can introduce the words 'subgroup' and 'isomorphic groups' as the standard terminology for what the learners have discovered for themselves.
Key Questions
What happens when you combine two reflections in intersecting mirror lines?
What transformation results when you combine a reflection in a mirror line and a rotation about a point on the mirror line?
What is the same and what is different about the groups with two elements that contain the identity and reflection in a single mirror line?
Possible extension
The challenge is so structured that it could be a short activity leading on to a similar investigation of the symmetries of a cylinder and finding out why there are only seven frieze groups. See Paint Rollers for Frieze Patterns.
To explore the ideas of groups of transformations further you could read the article Grouping Transformations.
Possible support
The three challenges: Decoding Transformations, Combining Transformations and Simplifying Transformations introduce the idea of an 'algebra' to record transformations and the way transformations combine to give other transformations.
