Exploring and noticing

problem

Inequalities

Age

16 to 18

Challenge level

Which of the statements must be true?
problem

The Koch Snowflake

Age

16 to 18

Challenge level

Explore the strange geometrical properties of the Koch Snowflake.
problem

Polite Numbers

Age

16 to 18

Challenge level

A polite number can be written as the sum of two or more consecutive positive integers, for example 8+9+10=27 is a polite number. Can you find some more polite, and impolite, numbers?
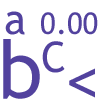problem

What Do Functions Do for Tiny X?

Age

16 to 18

Challenge level

Looking at small values of functions. Motivating the existence of the Maclaurin expansion.
problem

Impossible Triangles?

Age

16 to 18

Challenge level

Which of these triangular jigsaws are impossible to finish?
problem

Farey Neighbours

Age

16 to 18

Challenge level

Farey sequences are lists of fractions in ascending order of magnitude. Can you prove that in every Farey sequence there is a special relationship between Farey neighbours?
problem

Nine Eigen

Age

16 to 18

Challenge level

Explore how matrices can fix vectors and vector directions.
problem

Inverting Rational Functions

Age

16 to 18

Challenge level

Consider these questions concerning inverting rational functions
problem

Integral Arranging

Age

16 to 18

Challenge level

How would you sort out these integrals?
problem

How Fast Does It Grow?

Age

16 to 18

Challenge level

Exponential functions grow pretty quickly...