article
Magic squares
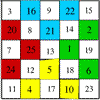An account of some magic squares and their properties and and how to construct them for yourself.
Conjecturing and generalising
-
-
articleWhy stop at three by one
Beautiful mathematics. Two 18 year old students gave eight different proofs of one result then generalised it from the 3 by 1 case to the n by 1 case and proved the general result.
-
articleSum the series
This article by Alex Goodwin, age 18 of Madras College, St Andrews describes how to find the sum of 1 + 22 + 333 + 4444 + ... to n terms. -
gameFavouriteDicey operations in line
Age7 to 11Challenge level
In these addition, subtraction, multiplication and division games, you'll need to think strategically to get closest to the target.
-
gameFavouriteDicey operations
Age7 to 14Challenge level
In these addition and subtraction games, you'll need to think strategically to get closest to the target.
-
gameFavouriteThe remainders game
Age7 to 14Challenge level
Play this game and see if you can figure out the computer's chosen number.
-
gameFavouriteFactors and multiples game
Age7 to 16Challenge level
A game in which players take it in turns to choose a number. Can you block your opponent?
-
gameSliding puzzle
Age11 to 16Challenge level
The aim of the game is to slide the green square from the top right hand corner to the bottom left hand corner in the least number of moves. -
gameJam
Age14 to 16Challenge level
To avoid losing think of another very well known game where the patterns of play are similar.
-
gameOne, three, five, seven
Age11 to 16Challenge level
A game for 2 players. Set out 16 counters in rows of 1,3,5 and 7. Players take turns to remove any number of counters from a row. The player left with the last counter looses.