Conjecturing and generalising
-
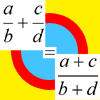 problemWhen if ever do you get the right answer if you add two fractions by adding the numerators and adding the denominators?
problemWhen if ever do you get the right answer if you add two fractions by adding the numerators and adding the denominators? -
 problem
problemLots of lollies
Frances and Rishi were given a bag of lollies. They shared them out evenly and had one left over. How many lollies could there have been in the bag?
-
 problem
problemShare bears
Yasmin and Zach have some bears to share. Which numbers of bears can they share so that there are none left over?
-

-
 problem
problemThe bridges of Konigsberg
Investigate how networks can be used to solve a problem for the 18th Century inhabitants of Konigsberg.
-
 problem
problemTourism
If you can copy a network without lifting your pen off the paper and without drawing any line twice, then it is traversable. Decide which of these diagrams are traversable.
-
 problem
problemPainted cube
Imagine a large cube made from small red cubes being dropped into a pot of yellow paint. How many of the small cubes will have yellow paint on their faces?
-
 problem
problemTilted squares
It's easy to work out the areas of most squares that we meet, but what if they were tilted?
-
 problem
problemCoordinate patterns
Charlie and Alison have been drawing patterns on coordinate grids. Can you picture where the patterns lead?
-
 problem
problemSeven squares - group-worthy task
Choose a couple of the sequences. Try to picture how to make the next, and the next, and the next... Can you describe your reasoning?
