How many miles to go?
How many more miles must the car travel before the numbers on the milometer and the trip meter contain the same digits in the same order?
Problem
How Many Miles to Go? printable sheet
A car's milometer reads $4631$ miles and the trip meter has $173.3$ on it:
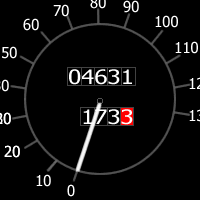
How many more miles must the car travel before the two numbers contain the same digits in the same order?
Can you find some other starting numbers that will lead to matching pairs?
What is the relationship between two starting numbers that will work?
If the milometer and trip meters had the following exact readings ($4632$ and $173.3$) then the two numbers will not contain the same digits in the same order before the milometer reaches $99999$ miles. Why is this?
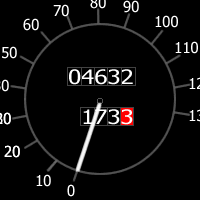
If the milometer 'loops the clock' back to $00000$ again at $100,000$ miles and the trip meter loops the clock back to $000.0$ at $1000$ miles, will the two numbers ever contain the same digits in the same order?
Getting Started
After one mile the milometer will read $4632$ and the trip meter will read $174.3$.
What happens when you add $10$ miles ... $100$ miles ... to each of the two measurements?
What are the two readings that match? Is it significant that one number is a multiple of the other?
Student Solutions
We received very contrasting approaches to solving this problem. Rami from Pierre Laporte School approached this in stages:
Well, you start with 4631 & 173.3
We'll add 2 to that, to get "3s" (in the far right hand columns): 4633 & 175.3
We'll add 300 to that one, to get "4s" (in the far left hand columns): 4933 & 475.3
We add 20 to that one: 4953 & 495.3
There's your answer ... 4953 & 495.3
Robert Stabler from Ardingly College Junior School used very similar reasoning:
In this problem I decided to alter the milometer until each single unit was the same as the trip meter's.
First I added 2 miles so they both ended in three.
I then added 20 so they both ended in 53.
Then I added 300 which made the milometer and trip meter end in 953.
They were now the same.
I added the numbers I had used up to 322.
Andrei Lazanu from School No. 205 in Bucharest realised that the two numbers would contain the same digits when the number on the milometer was ten times larger than the number on the trip meter, and then went on to generalise. This is how he arrived at the solution:
When you go a distance x, both the milometer and the trip meter will go a distance x.
The trip meter will need to have a value that is ten times smaller than the milometer, so I have:
4631 + x = 10(173.3 + x)
4631 + x = 1733 + 10x
9x = 2898
x =322 (miles)
So, you have to travel another 322 miles for the two numbers to have the same digits in the same order.
In the second situation, I have:
4632 + x = 10(173.3 + x)
4632 + x = 1733 + 10x
9x = 2899
2899 isn't divisible by 9.
In general, if m is the value indicated by the milometer and t the value indicated by the trip meter and x the distance travelled after the measurement, the possibilities are:
m +x = t + x$\rightarrow$ m = t $\rightarrow$ the first trip of the car (very difficult and rare)
Any distance is possible.
m + x = 10(t + x) $\rightarrow$ m + x = 10t + 10x $\rightarrow$ 9x = m -10t
This is the most common possibility.
(m - 10t) must be divisible by 9.
Here are some possibilities that will lead to matching pairs:
m = 1653; t = 60.0 $\rightarrow$ x = 117 (miles)
m = 5330; t = 1.1 $\rightarrow$ x = 591 (miles)
m = 9442, t = 10.0 $\rightarrow$ x = 1038 (miles)
m + x = 100(t + x) $\rightarrow$ m + x = 100t + 100x $\rightarrow$ 99x = m -100t
(m - 100t) must be divisible by 99.
Here are two possibilities that will lead to matching pairs:
m = 596; t = 2.00 $\rightarrow$ x = 4 (miles)
m = 7758; t = 36.00 $\rightarrow$ x = 42 (miles)
m + x = 1000(t + x) $\rightarrow$ m + x = 1000t + 1000x = 999x = m - 1000t
This solution is very rare, as the result must be divisible by 999, t must be a small one-digit number.
Teachers' Resources
Why do this problem?
This problem offers an interesting and challenging exercise in place value. It can be solved using an experimental approach or more formally using algebra. The task offers rich extension possibilities exploring a context for 'clock arithmetic'.
Possible approach
Ask students to work in pairs to decide what the two meters will read after 1 mile, 10 miles, and 100 miles, and then give them time to consider the first part of the problem. There is likely to be some confusion because of the presence of 1/10ths of a mile on just one of the meters. Some students could be asked to feedback on what was tricky/hard to explain/ hard to agree on.
In order to establish a good approach to these questions, ask a few different pairs to demonstrate their first ideas/full reasoning at the board. Then ask all students to derive the answer (4953) writing it out clearly, before making up their own initial meter readings and calculating how far they must go before the meters match.
On the board put the headings "these pairs of meters will never match" and "these will match". Students can record pairs of initial values for their peers to check. At some stage you'll probably need to declare the no-matches list, closed. Students who feel stuck could take a little break to test these 'solutions' and to try to observe what is making them work.
Some students might like to try to develop an algebraic expression for the distances. How can the question be rephrased as an equation?
Key questions
- What is the shortest trip that will cause the milometer to change? What effect will this have on the trip meter?
- How can we get the last digit to match?
Possible support
You could start students off with a simpler question, e.g. if the trip meter registered 000.0 miles and the milometer registered 00009 miles or 00234 miles, how many miles would the car have to travel for the digits to work? When working on the starting question (4631 etc) allow a lot of time for trial and error solutions, encouraging paired discussions on how to make a better trial each time.
Encourage students to lay out the readings from the two dials in place-value columns and to work one step at a time, recording each new reading in turn.
Possible extension
- What happens when the car has travelled more than 10,000 miles? Does this allow any more possible starting numbers?
- What journeys leave the digits on both clocks unchanged?
