Conjecturing and generalising
-
 problemThe number of plants in Mr McGregor's magic potting shed increases overnight. He'd like to put the same number of plants in each of his gardens, planting one garden each day. How can he do it?
problemThe number of plants in Mr McGregor's magic potting shed increases overnight. He'd like to put the same number of plants in each of his gardens, planting one garden each day. How can he do it? -
 problem
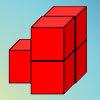
problemBrush loads
How can you arrange the 5 cubes so that you need the smallest number of Brush Loads of paint to cover them? Try with other numbers of cubes as well.
-
 problem
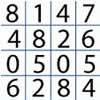
problemTables without tens
Investigate and explain the patterns that you see from recording just the units digits of numbers in the times tables. -
-
 problem
problemLitov's mean value theorem
Start with two numbers and generate a sequence where the next number is the mean of the last two numbers...
-

-
 problem
problemHarmonic triangle
Can you see how to build a harmonic triangle? Can you work out the next two rows?
-

-
 problem
problemThe better choice
Here are two games you can play. Which offers the better chance of winning?
-
 problem
problemCosy corner
Six balls are shaken. You win if at least one red ball ends in a corner. What is the probability of winning?
