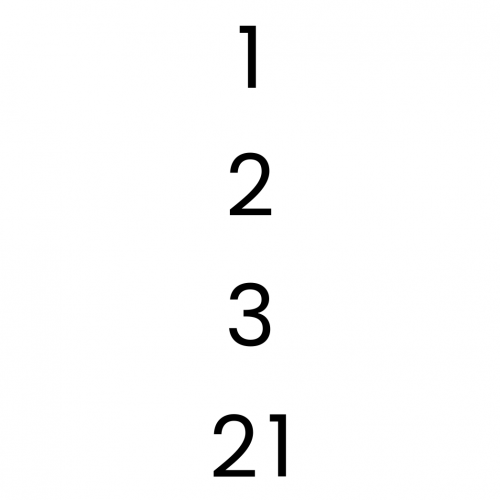
Factor lines
Arrange the four number cards on the grid, according to the rules, to make a diagonal, vertical or horizontal line.
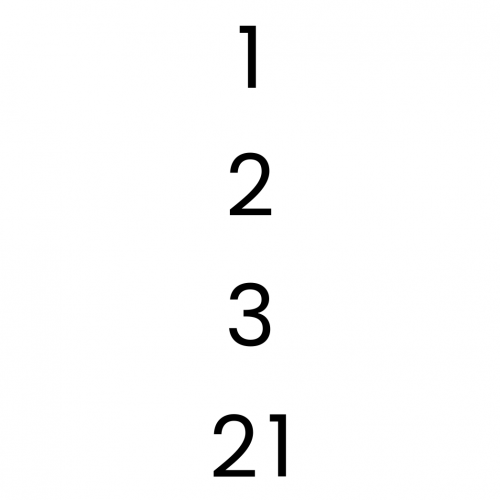
Arrange the four number cards on the grid, according to the rules, to make a diagonal, vertical or horizontal line.
Ten cards are put into five envelopes so that there are two cards in each envelope. The sum of the numbers inside it is written on each envelope. What numbers could be inside the envelopes?

I'm thinking of a number. My number is both a multiple of 5 and a multiple of 6. What could my number be?
On the graph there are 28 marked points. These points all mark the vertices (corners) of eight hidden squares. Can you find the eight hidden squares?
A task which depends on members of the group noticing the needs of others and responding.

Can you make doughnuts by matching these fractions, decimals and percentages?

Which pairs of cogs let the coloured tooth touch every tooth on the other cog? Which pairs do not let this happen? Why?
Watch our videos of multiplication methods that you may not have met before. Can you make sense of them?
