Doughnut Percents
Can you make doughnuts by matching these fractions, decimals and percentages?
Problem
This activity is designed to be tackled in pairs or small groups, but can also be completed individually. For more information on how this can be done in groups, take a look at the teachers' resources.
These printable domino cards can be put together to make four 'doughnuts' of four dominoes. The ends of dominoes which join together need to have equal value.
For example, a doughnut could look like this:
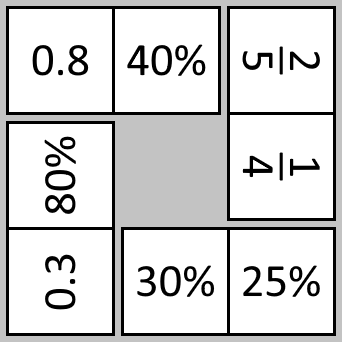
Have a go at making the four doughnuts. What do you notice?
Once you've made four doughnuts, you might like to try using the same set of cards to make two large doughnuts instead, with eight dominoes in each doughnut.
Is it possible to make one very large doughnut, using all sixteen cards? And if it is possible, is there more than one way of doing this? How many can you find?
Student Solutions
Well done to everybody who made these doughnuts. There were several slightly different possible answers for each of the three parts of this problem, and on this page we'll be focusing on different techniques for finding correct solutions rather than describing every possible answer. The percentages $66\frac{2}{3}$% and $33\frac{1}{3}$% tripped some people up - these ones are equivalent to $0.\dot{6}$ and $0.\dot{3}$, rather than $0.6$ and $0.3$.
Maya, Myla and Quinn from the Harrodian School in the UK explained the technique they used to make the doughnuts:
When we were solving the donuts, we converted all the numbers to percentages, making everything 10 times easier! After we matched all the numbers to their matching pairs and in no time, we completed the doughnuts!
This does sound like it would make things simpler. Eva from Twyford School in the UK had a different technique for keeping track of which dominoes matched:

This makes it very easy to see what's going on! I think Eva could have chosen the same colour for a couple more of these - can you see which ones?
Akhil from Cannon Lane Primary School in the UK started with one domino and looked for matches for it, working around the doughnut:
I have solved all three problems using the same method. Start with any one domino and then find another two dominoes that match each part of the first domino and so on. Going by the same reasoning, there can be 16 solutions for making one large doughnut as we could start using any one of the 16 domino cards.
Take a look at Akhil's full solution to see the doughnuts of each size that they made. I think Akhil is thinking of the 16 different solutions as being rotations of the same solution, but Grace and Emma from Harrodian found a completely different solution by putting the two $\frac{1}{4}$ dominoes together. They said:
We put to the side certain pairs/groups of numbers that had to be together then used a bit of trial and error at the end to connect the groups of numbers.

Ishan from Pierrepont Gamston Primary School in the UK explained how to go from small doughnuts to larger doughnuts:
First you work with $66\frac{2}{3}$% which is equivalent to 0.666666. Then you find out the other 3 etc. After you find out the first 4 donuts you can find a match for a start and an end of two of the donuts you can make two whole working donuts like that. Using the same technique, you can create a line with the first and last donuts matching and once you turn it into a donut you have one large donut.
Take a look at Ishan's full solution. The four small doughnuts are the same as Akhil's, but the large doughnut is different from both Akhil's and Grace and Emma's!
Keita, Kazuto, Oscar and Aarav from St. Mary's International School in Tokyo, Japan explained their thought process:
Four doughnuts:
We first started making the bottom left doughnut. We used the domino that says $10%$ and $\frac{3}{10}$ at first. Then, we noticed that $30%$ is equivalent to $\frac{3}{10}$. After that, we calculated that $90%$ is equivalent to $\frac{9}{10}$. $\frac{3}{4}$ is equivalent to $75%$ and $\frac{1}{10}$ is equivalent to $10%$. We easily made one doughnut! We did this for the other doughnuts and we were easily able to make four doughnuts.
Two doughnuts:
We solved this problem by putting them all into decimals for example, $30%$ is equivalent to $0.3$ because $100$ divided by $30$ equals $0.3$. We started with the left doughnut. $10%$ is equivalent to $\frac{1}{10}$ and $\frac{3}{4}$ is equivalent to $75%$ and $90%$ is equivalent to $\frac{9}{10}$ and so on.
One large doughnut:
We solved this problem together by first finding a single block to start with; in this example we started with the tile $66\frac{2}{3}$% and $\frac{1}{5}$. Next, we found the tile matching with $66\frac{2}{3}$%: $0.6$ recurring. Then we continued with this pattern occasionally editing the square to match the requirements of the problem.
Take a look at Keita, Kazuto, Oscar and Aarav's full solution. Their large doughnut is different to all the other ones we've featured on this page so far!
We also received similar solutions from: Yawin from St Faith's School in the UK; Emily, Lexie, Lily and Olivia from Irvinestown Primary School in the UK; Luke, who is home educated; Lexie and Harumi from ESF in Hong Kong; and Jack, Leo and Jack from Twyford School in England. Thank you all for sharing your ideas with us.
Teachers' Resources
Why do this problem?
This problem provides an opportunity for students to work together collaboratively to find equivalent fractions, decimals and percentages.
Possible approach
Key questions
Can you give any good examples of when someone noticed what you needed and tried to help?
Possible support
Set A from Matching Fractions, Decimals and Percentages would be a suitable introductory problem.
Possible extension
The dominoes can also be arranged into a pair of doughnuts or one large doughnut. Ask the team to create these shapes.
Sets B and C from Matching Fractions, Decimals and Percentages would be a suitable follow-up problem.
