3D shapes and their properties

problem

Three Cubed

Age

7 to 11

Challenge level

Can you make a 3×3 cube with these shapes made from small cubes?
problem

A Chain of Eight Polyhedra

Age

7 to 11

Challenge level

Can you arrange the shapes in a chain so that each one shares a face (or faces) that are the same shape as the one that follows it?
problem

Triangular Faces

Age

7 to 11

Challenge level

This problem invites you to build 3D shapes using two different triangles. Can you make the shapes from the pictures?
problem

Tetrahedron Faces

Age

7 to 11

Challenge level

One face of a regular tetrahedron is painted blue and each of the remaining faces are painted using one of the colours red, green or yellow. How many different possibilities are there?
problem

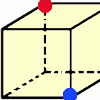Redblue

Age

7 to 11

Challenge level

Investigate the number of paths you can take from one vertex to another in these 3D shapes. Is it possible to take an odd number and an even number of paths to the same vertex?
problem

Auditorium Steps

Age

7 to 14

Challenge level

What is the shape of wrapping paper that you would need to completely wrap this model?
problem

Icosian Game

Age

11 to 14

Challenge level

This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only returning to the vertex you started at.
problem

Dodecawhat

Age

14 to 16

Challenge level

Follow instructions to fold sheets of A4 paper into pentagons and assemble them to form a dodecahedron. Calculate the error in the angle of the not perfectly regular pentagons you make.
problem

Proximity

Age

14 to 16

Challenge level

We are given a regular icosahedron having three red vertices. Show that it has a vertex that has at least two red neighbours.
problem

Moving Squares

Age

14 to 16

Challenge level

How can you represent the curvature of a cylinder on a flat piece of paper?