2D shapes and their properties

problem
Favourite

Hex

Age

11 to 14

Challenge level

Explain how the thirteen pieces making up the regular hexagon shown in the diagram can be re-assembled to form three smaller regular hexagons congruent to each other.
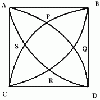
problem
Favourite

Quadarc

Age

14 to 16

Challenge level

Given a square ABCD of sides 10 cm, and using the corners as centres, construct four quadrants with radius 10 cm each inside the square. The four arcs intersect at P, Q, R and S. Find the area enclosed by PQRS.
problem
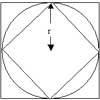
Favourite

Approximating Pi

Age

14 to 18

Challenge level

By inscribing a circle in a square and then a square in a circle find an approximation to pi. By using a hexagon, can you improve on the approximation?
problem
Favourite

Always, Sometimes or Never? KS1

Age

5 to 7

Challenge level

Are these statements relating to calculation and properties of shapes always true, sometimes true or never true?
problem
Favourite

Shapely Lines

Age

5 to 7

Challenge level

This challenge invites you to create your own picture using just straight lines. Can you identify shapes with the same number of sides and decorate them in the same way?
problem
Favourite

What's Happening?

Age

5 to 7

Challenge level

Shapes are added to other shapes. Can you see what is happening? What is the rule?
problem
Favourite

Triangle or No Triangle?

Age

5 to 7

Challenge level

Here is a selection of different shapes. Can you work out which ones are triangles, and why?
problem
Favourite

Chain of Changes

Age

5 to 7

Challenge level

In this activity, shapes can be arranged by changing either the colour or the shape each time. Can you find a way to do it?
problem
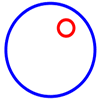
Favourite

2 Rings

Age

5 to 7

Challenge level

The red ring is inside the blue ring in this picture. Can you rearrange the rings in different ways? Perhaps you can overlap them or put one outside another?
problem
Favourite

Olympic Rings

Age

5 to 7

Challenge level

Can you design your own version of the Olympic rings, using interlocking squares instead of circles?